На этом шаге мы проанализируем указанную модель.

    Применительно к нашему одномерному массиву данных мы можем увидеть прогнозы для всех возможных значений признаков (рисунки 1 и 2). Для этого мы создаем тестовый набор данных и визуализируем полученные линии прогнозов:

[In 21]:
import numpy as np
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# создаем 1000 точек данных, равномерно распределенных между -3 и 3 
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
    # получаем прогнозы, используя 1, 3, и 9 соседей 
    reg = KNeighborsRegressor(n_neighbors=n_neighbors) 
    reg.fit(X_train, y_train) 
    ax.plot(line, reg.predict(line))
    ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
    ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
    ax.set_title(
        "{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(
            n_neighbors, reg.score(X_train, y_train), 
            reg.score(X_test, y_test)))
    ax.set_xlabel("Признак")
    ax.set_ylabel("Целевая переменная")
axes[0].legend(["Прогнозы модели", "Обучающие данные/ответы",
                "Тестовые данные/ответы"], loc="best")

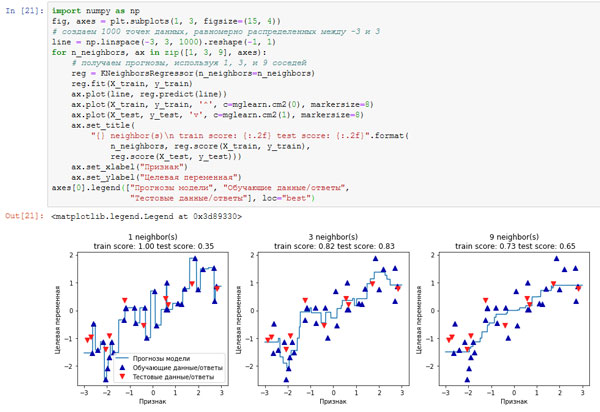
Рис.1. Сравнение прогнозов, полученных с помощью регрессии ближайших соседей для различных значений n_neighbors

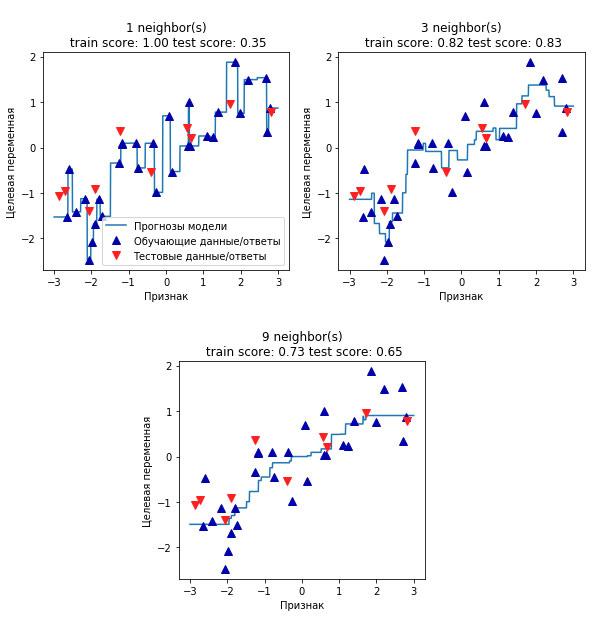
Рис.2. Отдельно графики

    Как видно на графике, при использовании лишь одного соседа каждая точка обучающего набора имеет очевидное влияние на прогнозы, и предсказанные значения проходят через все точки данных. Это приводит к очень неустойчивым прогнозам. Увеличение числа соседей приводит к получению более сглаженных прогнозов, но при этом снижается правильность подгонки к обучающим данным.

    Архив блокнота со всеми вычислениями, связанными с методом k ближайших соседей, можно взять здесь.

    На следующем шаге мы рассмотрим преимущества и недостатки этой модели.

Предыдущий шаг Содержание Следующий шаг