На этом шаге мы рассмотрим регрессионный вариант алгоритма.
Существует также регрессионный вариант алгоритма к ближайших соседей. Опять же, давайте начнем с рассмотрения одного ближайшего соседа, на этот раз воспользуемся набором данных wave. Мы добавили три точки тестового набора в виде зеленых звездочек по оси х. Прогноз с использованием одного соседа - это целевое значение ближайшего соседа. На рисунке 1 прогнозы показаны в виде синих звездочек:
[In 16]: mglearn.plots.plot_knn_regression(n_neighbors=1)
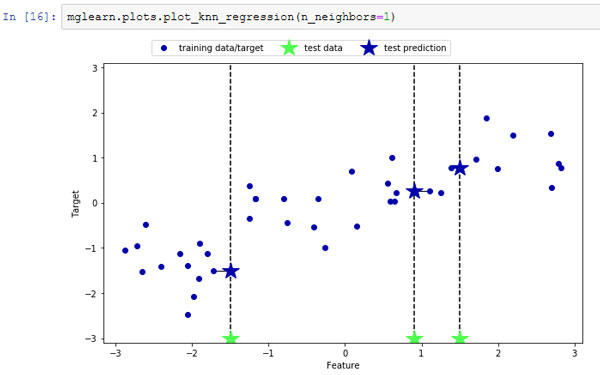
Рис.1. Прогнозы, полученные с помощью регрессионной модели одного ближайшего соседа для набора данных wave
И снова для регрессии мы можем использовать большее количество ближайших соседей. При использовании нескольких ближайших соседей прогнозом становится среднее значение соответствующих соседей (рисунок 2):
[In 17]: mglearn.plots.plot_knn_regression(n_neighbors=3)
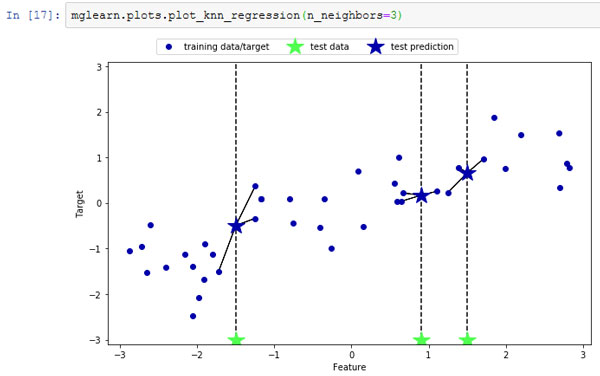
Рис.2. Прогнозы, полученные с помощью регрессионной модели трех ближайших соседей для набора данных wave
Алгоритм регрессии к ближайших соседей реализован в классе KNeighborsRegressor. Он используется точно так же, как KNeighborsClassifier:
[In 18]: from sklearn.neighbors import KNeighborsRegressor X, y = mglearn.datasets.make_wave(n_samples=40) # разбиваем набор данных wave на обучающую и тестовую выборки X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) # создаем экземпляр модели и устанавливаем количество соседей равным 3 reg = KNeighborsRegressor(n_neighbors=3) # подгоняем модель с использованием обучающих данных и обучающих ответов reg.fit(X_train, y_train) [Out 18]: KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=3, p=2, weights='uniform')
А теперь получим прогнозы для тестового набора.
[In 19]: print("Прогнозы для тестового набора:\n{}".format(reg.predict(X_test))) Прогнозы для тестового набора: [-0.05396539 0.35686046 1.13671923 -1.89415682 -1.13881398 -1.63113382 0.35686046 0.91241374 -0.44680446 -1.13881398]
Кроме того, мы можем оценить качество модели с помощью метода score, который для регрессионных моделей возвращает значение R2. R2, также известный как коэффициент детерминации, является показателем качества регрессионной модели и принимает значения от 0 до 1. Значение 1 соответствует идеальной прогнозирующей способности, а значение 0 соответствует константе модели, которая лишь предсказывает среднее значение ответов в обучающем наборе, y_train:
[In 20]: print("R^2 на тестовом наборе: {:.2f}".format(reg.score(X_test, y_test))) R^2 на тестовом наборе: 0.83
В данном случае значение R2 составляет 0.83, что указывает на относительно хорошее качество подгонки модели.
На следующем шаге мы рассмотрим анализ модели KNeighborsRegressor.
