На этом шаге мы рассмотрим лассо и сравним ее с гребневой регрессией.
Альтернативой Ridge как метода регуляризации линейной регрессии является Lasso. Как и гребневая регрессия, лассо также сжимает коэффициенты до близких к нулю значений, но несколько иным способом, называемым L1 регуляризацией. Результат L1 регуляризации заключается в том, что при использовании лассо некоторые коэффициенты становятся равны точно нулю. Получается, что некоторые признаки полностью исключаются из модели. Это можно рассматривать как один из видов автоматического отбора признаков. Получение нулевых значений для некоторых коэффициентов часто упрощает интерпретацию модели и может выявить наиболее важные признаки вашей модели.
Давайте применим метод лассо к расширенному набору данных Boston Housing:
[In 22]: import numpy as np from sklearn.linear_model import Lasso lasso = Lasso().fit(X_train, y_train) print("Правильность на обучающем наборе: {:.2f}".format(lasso.score(X_train, y_train))) print("Правильность на контрольном наборе: {:.2f}".format(lasso.score(X_test, y_test))) print("Количество использованных признаков: {}".format(np.sum(lasso.coef_ != 0))) Правильность на обучающем наборе: 0.29 Правильность на контрольном наборе: 0.21 Количество использованных признаков: 4
Как видно из сводки, Lasso дает низкую правильность как на обучающем, так и на тестовом наборе. Это указывает на недообучение и мы видим, что из 105 признаков используются только 4. Как и Ridge, Lasso также имеет параметр регуляризации alpha, который определяет степень сжатия коэффициентов до нулевых значений. В предыдущем примере мы использовали значение по умолчанию alpha=1.0. Чтобы снизить недообучение, давайте попробуем уменьшить alpha. При этом нам нужно увеличить значение max_iter (максимальное количество итераций):
[In 23]: # мы увеличиваем значение "max_iter", # иначе модель выдаст предупреждение, что нужно увеличить max_iter. lasso001 = Lasso(alpha=0.01, max_iter=10000).fit(X_train, y_train) print("Правильность на обучающем наборе: {:.2f}".format(lasso001.score(X_train, y_train))) print("Правильность на тестовом наборе: {:.2f}".format(lasso001.score(X_test, y_test))) print("Количество использованных признаков: {}".format(np.sum(lasso001.coef_ != 0))) Правильность на обучающем наборе: 0.90 Правильность на тестовом наборе: 0.77 Количество использованных признаков: 33
Более низкое значение alpha позволило нам получить более сложную модель, которая продемонстрировала более высокую правильность на обучающем и тестовом наборах. Лассо работает немного лучше, чем гребневая регрессия, и мы используем лишь 33 признака из 105. Это делает данную модель более легкой с точки зрения интерпретации.
Однако, если мы установим слишком низкое значение alpha, мы снова нивелируем эффект регуляризации и получим в конечном итоге переобучение, придя к результатам, аналогичным результатам линейной регрессии:
[In 24]: lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train) print("Правильность на обучающем наборе: {:.2f}".format(lasso00001.score(X_train, y_train))) print("Правильность на тестовом наборе: {:.2f}".format(lasso00001.score(X_test, y_test))) print("Количество использованных признаков: {}".format(np.sum(lasso00001.coef_ != 0))) равильность на обучающем наборе: 0.95 Правильность на тестовом наборе: 0.64 Количество использованных признаков: 96
Опять же, мы можем построить графики для коэффициентов различных моделей, аналогичные рисунку 3 предыдущего шага:
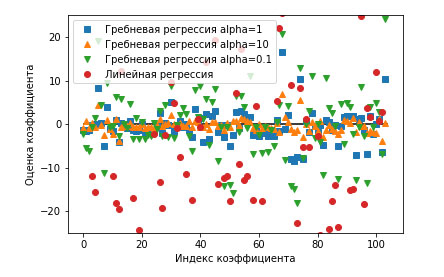
Рис.1. Рисунок 3 предыдущего шага, содержащий сравнение оценок коэффициентов гребневой регрессии с разными значениями alpha и линейной регрессии
Результат приведен на рисунках 2 и 3.
[In 25]: plt.plot(lasso.coef_, 's', label="Лассо alpha=1") plt.plot(lasso001.coef_, '^', label="Лассо a1pha=0.01") plt.plot(lasso00001.coef_, 'v', label="Лассо alpha=0.0001") plt.plot(ridge01.coef_, 'o', label="Гребневая регрессия alpha=0.1") plt.legend(ncol=2, loc=(0, 1.05)) plt.ylim(-25, 25) plt.xlabel("Индекс коэффициента") plt.ylabel("Оценка коэффициента")
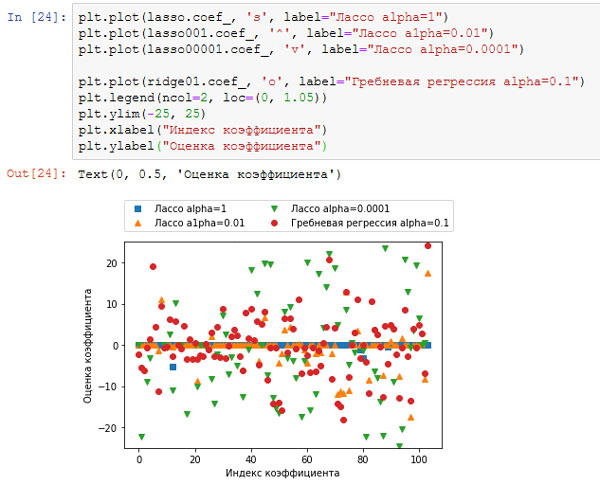
Рис.2. Сравнение коэффициентов для лассо-регресии с разными значениями alpha и гребневой регрессии
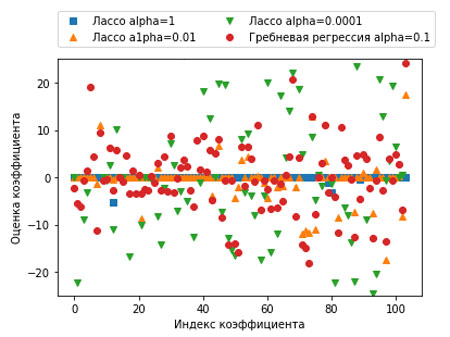
Рис.3. Отдельно график
Для alpha=1 мы видим, что не только большинство коэффициентов равны нулю (что мы уже знали), но и остальные коэффициенты также малы по величине. Уменьшив alpha до 0.01, получаем решение, показанное в виде оранжевых треугольников, большая часть коэффициентов для признаков становятся в точности равными нулю. При alpha=0.0001 мы получаем практически нерегуляризированную модель, у которой большинство коэффициентов отличны от нуля и имеют большие значения. Для сравнения приводится наилучшее решение, полученное с помощью гребневой регрессии. Модель Ridge с alpha=0.1 имеет такую же прогностическую способность, что и модель лассо с alpha=0.01, однако при использовании гребневой регрессии все коэффициенты отличны от нуля.
На практике, когда стоит выбор между гребневой регрессией и лассо, предпочтение, как правило, отдается гребневой регрессии. Однако, если у вас есть большое количество признаков и есть основания считать, что лишь некоторые из них важны, Lasso может быть оптимальным выбором. Аналогично, если вам нужна легко интерпретируемая модель, Lasso поможет получить такую модель, так как она выберет лишь подмножество входных признаков. В библиотеке scikit-learn также имеется класс ElasticNet, который сочетает в себе штрафы Lasso и Ridge. На практике эта комбинация работает лучше всего, впрочем, это достигается за счет двух корректируемых параметров: один для L1 регуляризации, а другой - для L2 регуляризации.
На следующем шаге мы рассмотрим линейные модели для классификации.
