На этом шаге мы рассмотрим использование линейных моделей в задачах классификации.

Линейные модели также широко используются в задачах классификации. Давайте посмотрим сначала на бинарную классификацию. В этом случае прогноз получают с помощью следующей формулы:

  y = w[0] * x[0] + w[1] * x[1] +... + w[p] * x[p] + b > 0

Формула очень похожа на формулу линейной регрессии, но теперь вместо того, чтобы просто возвратить взвешенную сумму признаков, мы задаем для прогнозируемого значения порог, равный нулю. Если функция меньше нуля, мы прогнозируем класс -1, если она больше нуля, мы прогнозируем класс +1. Это прогнозное правило является общим для всех линейных моделей классификации. Опять же, есть много различных способов найти коэффициенты (w) и константу (b).

Для линейных моделей регрессии выход у является линейной функцией признаков:

линией,
плоскостью или
гиперплоскостью (для большого количества измерений).

Для линейных моделей классификации граница принятия решений (decision boundary) является линейной функцией аргумента. Другими словами, (бинарный) линейный классификатор - это классификатор, который разделяет два класса с помощью линии, плоскости или гиперплоскости. Здесь и далее мы приведем конкретные примеры.

Существует масса алгоритмов обучения линейных моделей. Два критерия задают различия между алгоритмами:

Измеряемые метрики качества подгонки обучающих данных;
Факт использования регуляризации и вид регуляризации, если она используется.

Различные алгоритмы по-разному определяют, что значит "хорошая подгонка обучающих данных". В силу технико-математических причин невозможно скорректировать w и b, чтобы минимизировать количество неверно классифицированных случаев, выдаваемое алгоритмами, как можно было бы надеяться. С точки зрения поставленных нами целей и различных сфер применения различные варианты метрик качества подгонки (так называемые функции потерь или loss functions) не имеют большого значения.

Двумя наиболее распространенными алгоритмами линейной классификации являются

логистическая регрессия (logistic regression), реализованная в классе linear_model.LogisticRegression, и
линейный метод опорных векторов (linear support vector machines) или линейный SVM, реализованный в классе svm.LinearSVC (SVC расшифровывается как support vector classifier - классификатор опорных векторов).

Несмотря на свое название, логистическая регрессия является алгоритмом классификации, а не алгоритмом регрессии, и его не следует путать с линейной регрессией.

Мы можем применить модели LogisticRegression и LinearSVC к набору данных forge и визуализировать границу принятия решений, найденную линейными моделями (рисунок 1):

[In 26]:
from sklearn.linear_model import LogisticRegression 
from sklearn.svm import LinearSVC

X, y = mglearn.datasets.make_forge()

fig, axes = plt.subplots(1, 2, figsize=(10, 3))

for model, ax in zip([LinearSVC(), LogisticRegression()], axes): 
    clf = model.fit(X, y)
    mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5, ax=ax, alpha=.7)
    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
    ax.set_title("{}".format(clf.__class__.__name__))
    ax.set_xlabel("Признак 0") 
    ax.set_ylabel("Признак 1")
axes[0].legend()

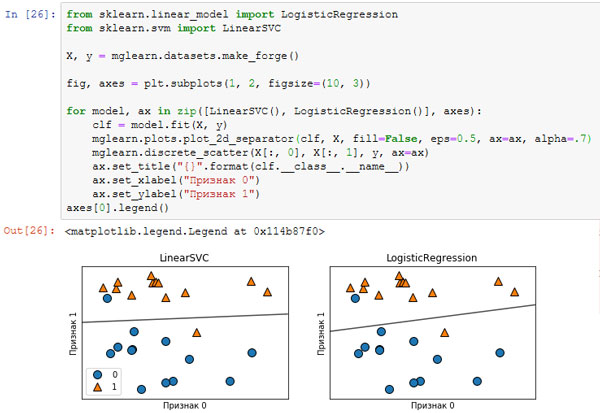
Рис.1. Границы принятия решений линейного SVM и логистической регрессии для набора данных forge (использовались значения параметров по умолчанию)

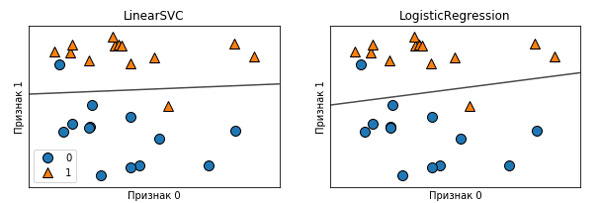
Рис.2. Отдельно графики

На этих рисунках, как и раньше, первый признак набора данных forge отложен по оси х, а второй признак - по оси у. Здесь показаны границы принятия решений, найденные LinearSVC и LogisticRegression соответственно. Они представлены в виде прямых линий, отделяющих область значений, классифицированных как класс 1 (в верхней части графика) от области значений, классифицированных как класс 0 (в нижней части графика). Другими словами, любая новая точка данных, которая лежит выше черной линии будет отнесена соответствующей моделью к классу 1, тогда как любая точка, лежащая ниже черной линии, будет отнесена к классу 0.

Обе модели имеют схожие границы принятия решений. Обратите внимание, что обе модели неправильно классифицировали две точки. По умолчанию обе модели используют L2 регуляризацию, тот же самый метод, который используется в гребневой регрессии.

Для LogisticRegression и LinearSVC компромиссный параметр, который определяет степень регуляризации, называется C, и более высокие значения C соответствуют меньшей регуляризации. Другими словами, когда вы используете высокое значение параметра C, LogisticRegression и LinearSVC пытаются подогнать модель к обучающим данным как можно лучше, тогда как при низких значениях параметра C модели делают больший акцент на поиске вектора коэффициентов (w), близкого к нулю.

Существует еще одна интересная деталь, связанная с работой параметра C. Использование низких значений C приводит к тому, что алгоритмы пытаются подстроиться под "большинство" точек данных, тогда как использование более высоких значений C подчеркивает важность того, чтобы каждая отдельная точка данных была классифицирована правильно. Ниже приводится иллюстрация использования LinearSVC (рисунок 3):

[In 27]:
mglearn.plots.plot_linear_svc_regularization()

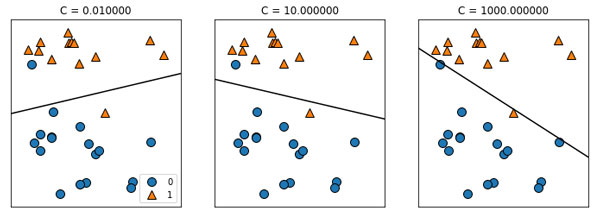
Рис.3. Границы принятия решений линейного SVM с различными значениями C для набора данных forge

На графике слева показана модель с очень маленьким значением C, соответствующим большой степени регуляризации. Большая часть точек класса 0 находятся в нижней части графика, а большинство точек класса 1 находятся в верхней части. Сильно регуляризованная модель дает относительно горизонтальную линию, неправильно классифицируя две точки. На центральном графике значение С немного выше и модель в большей степени фокусируется на двух неправильно классифицированных примерах, наклоняя границу принятия решений. Наконец, на графике справа очень высокое значение С модели наклоняет границу принятия решений еще сильнее, теперь правильно классифицируя все точки класса 0. Одна из точек класса 1 по-прежнему неправильно классифицирована, поскольку невозможно правильно классифицировать все наблюдения этого набора данных с помощью прямой линии. Модель на графике справа старается изо всех сил правильно классифицировать все точки, но не может дать хорошего обобщения сразу для обоих классов. Другими словами, эта модель скорее всего переобучена.

Как и в случае с регрессией, линейные модели классификации могут показаться слишком строгими в условиях низкоразмерного пространства, предлагая границы принятия решений в виде прямых линий или плоскостей. Опять же, при наличии большого числа измерений линейные модели классификации приобретают высокую прогнозную силу и с увеличением числа признаков защита от переобучения становится все более важной.

На следующем шаге мы закончим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг