На этом шаге мы рассмотрим использование линейных моделей для мультиклассовой клоссификации.
Многие линейные модели классификации предназначены лишь для бинарной классификации и не распространяются на случай мультиклассовой классификации (за исключением логистической регрессии). Общераспространенный подход, позволяющий распространить алгоритм бинарной классификации на случай мультиклассовой классификации называет подходом "один против остальных" (one-vs.-resf) (иногда его также называют "один против всех" (one-vs.-all)). В подходе "один против остальных" для каждого класса строится бинарная модель, которая пытается отделить этот класс от всех остальных, в результате чего количество моделей определяется количеством классов. Для получения прогноза точка тестового набора подается на все бинарные классификаторы. Классификатор, который выдает по своему классу наибольшее значение, "побеждает" и метка этого класса возвращается в качестве прогноза.
Используя бинарный классификатор для каждого класса, мы получаем один вектор коэффициентов (w) и одну константу (b) по каждому классу. Класс, который получает наибольшее значение согласно нижеприведенной формуле, становится присвоенной меткой класса:
w[0] * x[0] + w[1] * x[1] +... + w[p] * x[p] + b
Математический аппарат мультиклассовой логистической регрессии несколько отличается от подхода "один против остальных", однако он также дает один вектор коэффициентов и константу для каждого класса и использует тот же самый способ получения прогнозов.
Давайте применим метод "один против остальных" к простому набору данных с 3-классовой классификацией. Мы используем двумерный массив данных, где каждый класс задается данными, полученными из гауссовского распределения (рисунок 1):
[In 35]: from sklearn.datasets import make_blobs X, y = make_blobs(random_state=42) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) plt.xlabel("Признак 0") plt.ylabel("Признак 1") plt.legend(["Класс 0", "Класс 1", "Класс 2"])
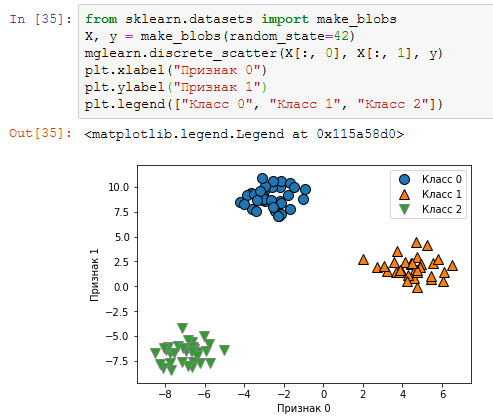
Рис.1. Двумерный синтетический набор данных, содержащий три класса
Теперь обучаем классификатор LinearSVC на этом наборе данных:
[In 36]: linear_svm = LinearSVC().fit(X, y) print("Форма коэффициента: ", linear_svm.coef_.shape) print("Форма константы: ", linear_svm.intercept_.shape) Форма коэффициента: (3, 2) Форма константы: (3,)
Мы видим, что атрибут coef_ имеет форму (3, 2), это означает, что каждая строка coef_ содержит вектор коэффициентов для каждого из трех классов, а каждый столбец содержит значение коэффициента для конкретного признака (в этом наборе данных их два). Атрибут intercept_ теперь является одномерным массивом, в котором записаны константы классов.
Давайте визуализируем линии (границы принятия решений), полученные с помощью трех бинарных классификаторов (рисунок 2):
[In 37]: mglearn.discrete_scatter(X[:, 0], X[:, 1], y) line = np.linspace(-15, 15) for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']): plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color) plt.ylim(-10, 15) plt.xlim(-10, 8) plt.xlabel("Признак 0") plt.ylabel("Признак 1") plt.legend(['Класс 0', 'Класс 1', 'Класс 2', 'Линия класса 0', 'Линия класса 1', 'Линия класса 2'], loc=(1.01, 0.3))
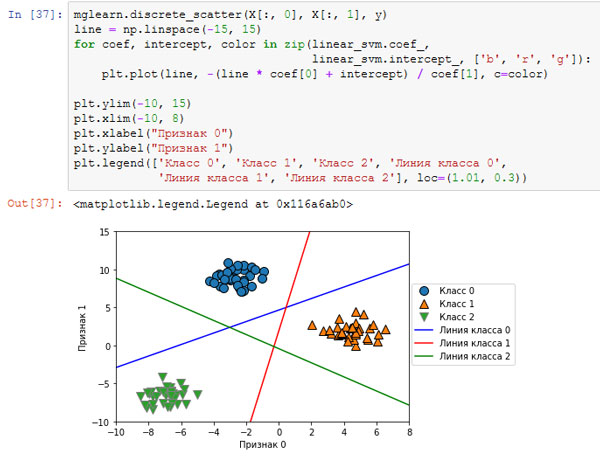
Рис.2. Границы принятия решений, полученные с помощью трех бинарных классификаторов в рамках подхода "один против остальных"
Видно, что все точки, принадлежащие классу 0 в обучающих данных, находятся выше линии, соответствующей классу 0. Это означает, что они отнесены к "классу 0" данного бинарного классификатора. Точки класса 0 находятся выше линии, соответствующей классу 2. Это означает, что они классифицируются бинарным классификатором для класса 2 как "остальные". Точки, принадлежащие классу 0, находятся слева от линии, соответствующей классу 1. Это означает, что бинарный классификатор для класса 1 также классифицирует их как "остальные". Таким образом, в итоге любая точка в этой области будет отнесена к классу 0 (результат, получаемый по формуле для классификатора 0, больше нуля, тогда как для двух остальных классов он меньше нуля).
Однако что насчет треугольника в середине графика? Все три бинарных классификатора относят точки, расположенные там, к "остальным". Какой класс будет присвоен точке, расположенной в треугольнике? Ответ - класс, получивший наибольшее значение по формуле классификации, то есть класс ближайшей линии.
Следующий пример (рисунок 3) показывает прогнозы для всех областей двумерного пространства:
[In 38]: mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) line = np.linspace(-15, 15) for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']): plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color) plt.legend(['Класс 0', 'Класс 1', 'Класс 2', 'Линия класса 0', 'Линия класса 1', 'Линия класса 2'], loc=(1.01, 0.3)) plt.xlabel("Признак 0") plt.ylabel("Признак 1")

Рис.3. Мультиклассовые границы принятия решений, полученные с помощью трех бинарных классификаторов в рамках подхода "один против остальных"
На следующем шаге мы рассмотрим преимущества, недостатки и параметры.
