На этом шаге мы рассмотрим более пдробно работу LogisticRegression.
Давайте более подробно разберем работу LogisticRegression на наборе данных Breast Cancer:
[In 28]: from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) logreg = LogisticRegression().fit(X_train, y_train) print("Правильность на обучающем наборе: {:.3f}".format(logreg.score(X_train, y_train))) print("Правильность на тестовом наборе: {:.3f}".format(logreg.score(X_test, y_test))) Правильность на обучающем наборе: 0.953 Правильность на тестовом наборе: 0.958
Значение по умолчанию C=1 обеспечивает неплохое качество модели, правильность на обучающем и тестовом наборах составляет 95%. Однако поскольку качество модели на обучающем и тестовом наборах примерно одинако, вполне вероятно, что мы недообучили модель. Давайте попробуем увеличить C, чтобы подогнать более гибкую модель:
[In 29]: ogreg100 = LogisticRegression(C=100).fit(X_train, y_train) print("Правильность на обучающем наборе: {:.3f}".format(logreg100.score(X_train, y_train))) print("Правильность на тестовом наборе: {:.3f}".format(logreg100.score(X_test, y_test))) Правильность на обучающем наборе: 0.974 Правильность на тестовом наборе: 0.965
Использование C=100 привело к более высокой правильности на обучающей выборке, а также немного увеличилась правильность на тестовой выборке, что подтверждает наш довод о том, что более сложная модель должна сработать лучше.
Кроме того, мы можем выяснить, что произойдет, если мы воспользуемся более регуляризованной моделью (установив C=0.01 вместо значения по умолчанию C=1):
[In 30]: logreg001 = LogisticRegression(C=0.01).fit(X_train, y_train) print("Правильность на обучающем наборе: {:.3f}".format(logreg001.score(X_train, y_train))) print("Правильность на тестовом наборе: {:.3f}".format(logreg001.score(X_test, y_test))) Правильность на обучающем наборе: 0.934 Правильность на тестовом наборе: 0.930
Как и следовало ожидать, когда мы получили недообученную модель и переместились влево по шкале, показанной на рисунке 1 27 шага, правильность как на обучающем, так и на тестовом наборах снизилась по сравнению с правильностью, которую мы получили, использовав параметры по умолчанию.
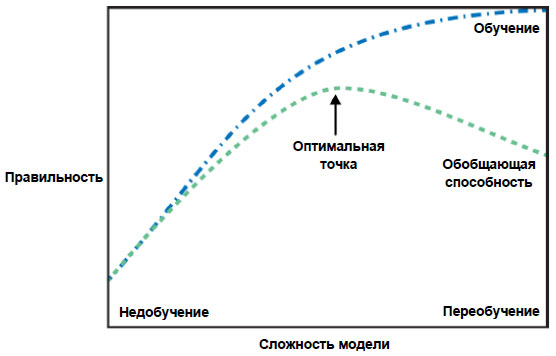
Рис.1. Рисунок 1 из 27 шага, иллюстрирующий компромисс между сложностью модели и правильностью на обучающей и тестовой выборках
И, наконец, давайте посмотрим на коэффициенты логистической регрессии, полученные с использованием трех различных значений параметра регуляризации C (рисунки 2 и 3):
[In 31]: plt.plot(logreg.coef_.T, 'o', label="C=1") plt.plot(logreg100.coef_.T, '^', label="C=100") plt.plot(logreg001.coef_.T, 'v', label="C=0.001") plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90) plt.hlines(0, 0, cancer.data.shape[1]) plt.ylim(-5, 5) plt.xlabel("Индекс коэффициента") plt.ylabel("Индекс коэффициента") plt.legend()
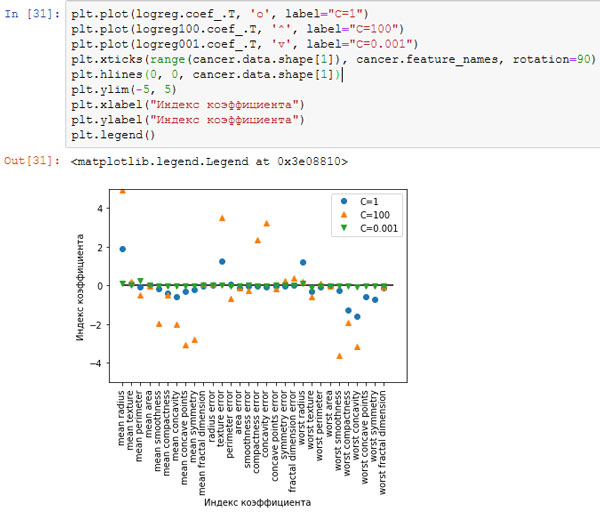
Рис.2. Коэффициенты, полученные с помощью логистической регрессии с разными значениями C для набора данных Breast Cancer
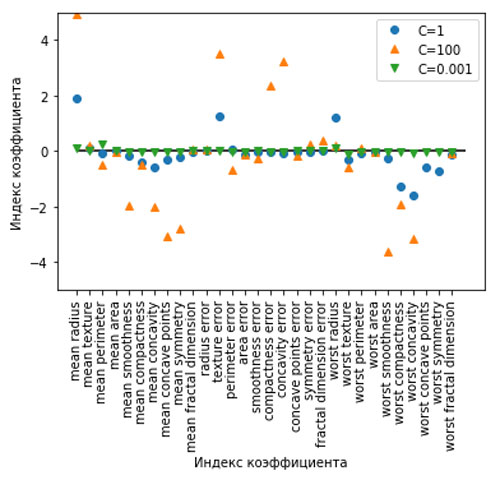
Рис.3. Только график
Поскольку LogisticRegression по умолчанию использует L2 регуляризацию, результат похож на результат, полученный при использовании модели Ridge
(рисунок 3 39 шага). Большая степень регуляризации сильнее сжимает коэффициенты к нулю, хотя коэффициенты никогда не станут в
точности равными нулю. Изучив график более внимательно, можно увидеть интересный эффект, произошедший с третьим коэффициентом, коэффициентом признака «mean perimeter».
При C=100 и C=1 коэффициент отрицателен, тогда как при C=0.001 коэффициент положителен, при этом его оценка больше, чем оценка коэффициента при C=1.
Когда мы интерпретируем данную модель, коэффициент говорит нам, какой класс связан с этим признаком. Возможно, что высокое значение признака «texture error» связано с примером,
классифицированным как «злокачественный». Однако изменение знака коэффициента для признака «mean perimeter» означает, что в зависимости от рассматриваемой модели
высокое значение «mean perimeter» может указывать либо на доброкачественную, либо на злокачественную опухоль. Приведенный пример показывает, что интерпретировать коэффициенты линейных
моделей всегда нужно с осторожностью и скептицизмом.
Если мы хотим получить более интерпретабельную модель, нам может помочь L1 регуляризация, поскольку она ограничивает модель использованием лишь нескольких признаков. Ниже приводится график с коэффициентами и оценками правильности для L1 регуляризации (рисунок 3):
[In 34]: for C, marker in zip([0.001, 1, 100], ['o', '^', 'v']): lr_l1 = LogisticRegression(C=C, penalty="l1").fit(X_train, y_train) print("Правильность на обучении для логрегрессии l1 с C={:.3f}: {:.2f}". format(C, lr_l1.score(X_train, y_train))) print("Правильность на тесте для логрегрессии l1 с C={:.3f}: {:.2f}". format(C, lr_l1.score(X_test, y_test))) plt.plot(lr_l1.coef_.T, marker, label="C={:.3f}".format(C)) plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90) plt.hlines(0, 0, cancer.data.shape[1]) plt.xlabel("Индекс коэффициента") plt.ylabel("Оценка коэффициента") plt.ylim(-5, 5) plt.legend(loc=3) Правильность на обучении для логрегрессии l1 с C=0.001: 0.91 Правильность на тесте для логрегрессии l1 с C=0.001: 0.92 Правильность на обучении для логрегрессии l1 с C=1.000: 0.96 Правильность на тесте для логрегрессии l1 с C=1.000: 0.96 Правильность на обучении для логрегрессии l1 с C=100.000: 0.99 Правильность на тесте для логрегрессии l1 с C=100.000: 0.98
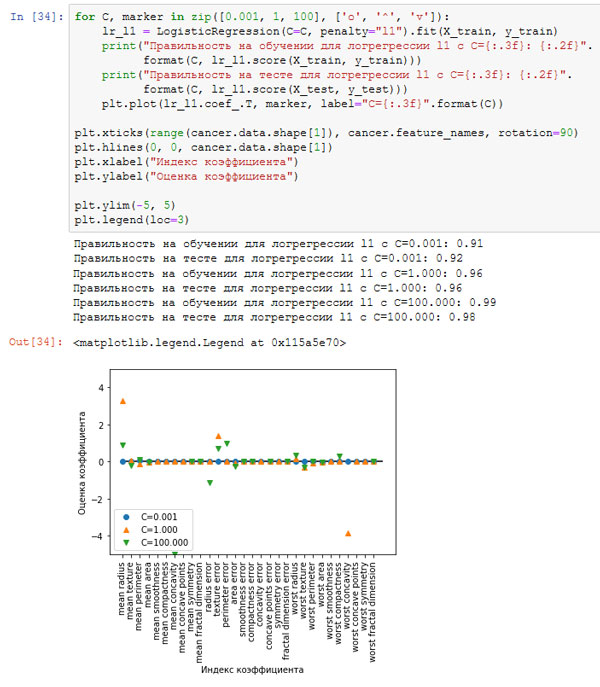
Рис.4. Коэффициенты логистической регрессии с L1 штрафом для набора данных Breast Cancer (использовались различные значения C)
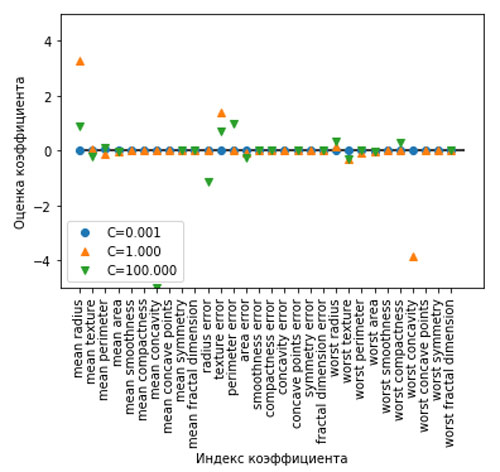
Рис.5. Только график
Видно, что существует много параллелей между линейными моделями для бинарной классификации и линейными моделями для регрессии. Как и в регрессии, основное различие между моделями – в параметре penalty, который влияет на регуляризацию и определяет, будет ли модель использовать все доступные признаки или выберет лишь подмножество признаков.
На следующем шаге мы рассмотрим линейные модели для мультиклассовой классификации.
