На этом шаге мы рассмотрим взаимосвязь линейных моделей и нелинейных признаков.
На рисунке 2 41 шага было видно, что в низкоразмерных пространствах линейные модели накладывают весьма жесткие ограничения, поскольку линии и гиперплоскости имеют ограниченную гибкость.
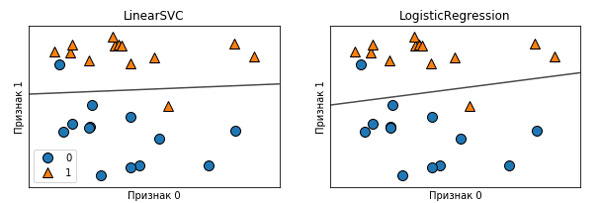
Рис.2 (41 шаг). Границы принятия решений линейного SVM и логистической регрессии для набора данных forge (использовались значения параметров по умолчанию)
Один из способов сделать линейную модель более гибкой - добавить новые признаки, например, добавить взаимодействия или полиномы входных признаков.
Давайте взглянем на синтетический набор данных, который мы использовали на 51 шаге "Важность признаков в деревьях" (см. рисунок 2 51 шага):
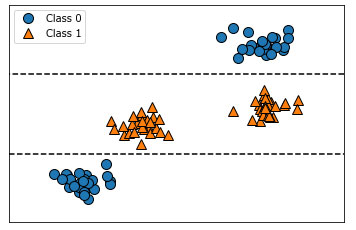
Рис.2 (51 шаг). Двумерный массив данных, в котором признак имеет немонотонную взаимосвязь с меткой класса, и границы принятия решений, найденные с помощью дерева
[In 2]: from sklearn.datasets import make_blobs X, y = make_blobs(centers=4, random_state=8) y = y % 2 mglearn.discrete_scatter(X[:, 0], X[:, 1], y) plt.xlabel("Признак 0") plt.ylabel("Признак 1")
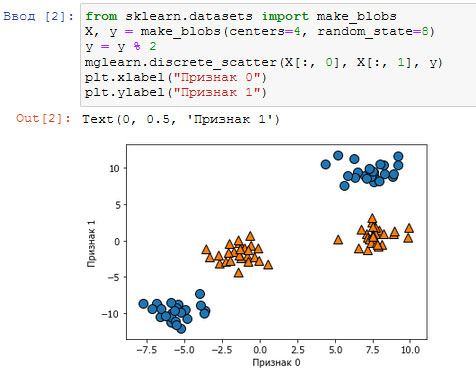
Рис.1. Набор данных с двухклассовой классификацией, в котором классы линейно неразделимы
Линейная модель классификации может отделить точки только с помощью прямой линии и не может дать хорошее качество для этого набора данных (см. рисунок 2 этого шага):
[In 3]: from sklearn.svm import LinearSVC linear_svm = LinearSVC().fit(X, y) mglearn.plots.plot_2d_separator(linear_svm, X) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) plt.xlabel("Признак 0") plt.ylabel("Признак 1")
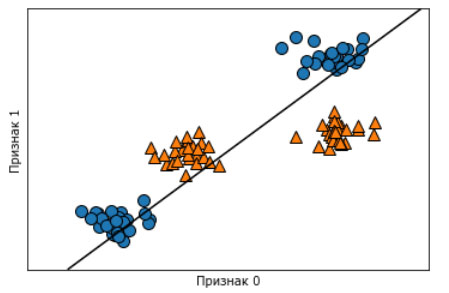
Рис.2. Граница принятия решений, найденная с помощью линейного SVM
Теперь давайте расширим набор входных признаков, скажем, добавим в качестве нового признака featurel ** 2, квадрат второго признака. Теперь каждую точку данных мы представим не в виде точки двумерного пространства (feature0, feature1), а виде точки трехмерного пространства (feature0, feature1, feature1 ** 2).
Мы добавили этот признак в иллюстративных целях. Этот выбор не является принципиально важным.
Новое пространство признаков показано на рисунке 3 в виде трехмерной диаграммы рассеяния:
[In 4]: # добавляем второй признак, возведенный в квадрат X_new = np.hstack([X, X[:, 1:] ** 2]) from mpl_toolkits.mplot3d import Axes3D, axes3d figure = plt.figure() # визуализируем в 3D ax = Axes3D(figure, elev=-152, azim=-26) # сначала размещаем на графике все точки с y == 0, затем с y == 1 mask = y == 0 ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60) ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=60) ax.set_xlabel("признак0") ax.set_ylabel("признак1") ax.set_zlabel("признак1 ** 2")
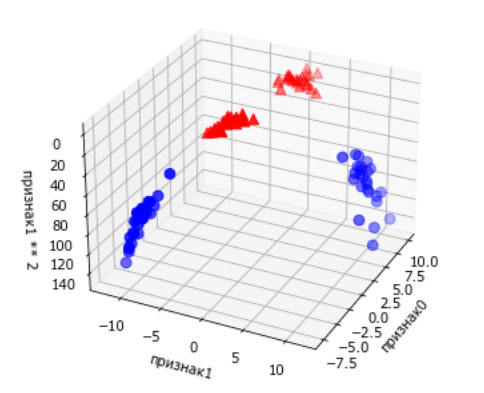
Рис.3. Расширение набора данных, показанного на рисунке 2, за счет добавления третьего признака, полученного на основе признака 1
В новом представлении данных уже можно отделить два класса друг от друга, используя линейную модель, плоскость в трехмерном пространстве. Мы можем убедиться в этом, подогнав линейную модель к дополненным данным (см. рисунок 4):
[In 5]: linear_svm_3d = LinearSVC().fit(X_new, y) coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_ # показать границу принятия решений линейной модели figure = plt.figure() ax = Axes3D(figure, elev=-152, azim=-26) xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50) yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50) XX, YY = np.meshgrid(xx, yy) ZZ = (coef[0] * XX + coef[1] * YY + intercept) / coef[2] ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3) ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=60) ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='b', marker='^', cmap=mglearn.cm2, s=60) ax.set_xlabel("признак0") ax.set_ylabel("признак1") ax.set_zlabel("признак1 ** 2")
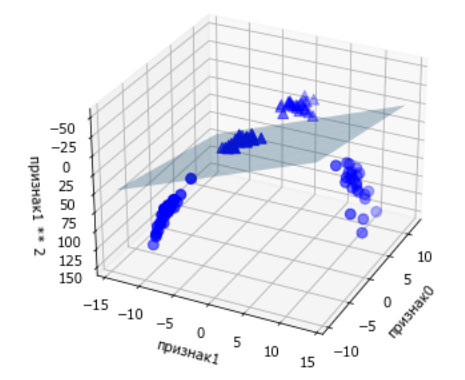
Рис.4. Граница принятия решений, найденная линейным SVM для расширенного трехмерного набора данных
Фактически модель линейного SVM как функция исходных признаков не является больше линейной. Это не линия, а скорее эллипс, как можно увидеть на графике, построенном ниже (рисунок 5):
[In 6]: ZZ = YY ** 2 dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()]) plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()], cmap=mglearn.cm2, alpha=0.5) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) plt.xlabel("Признак 0") plt.ylabel("Признак 1")
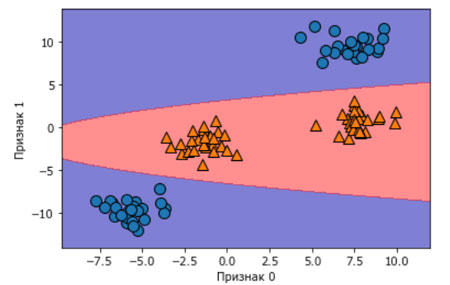
Рис.5. Граница принятия решений для рисунка 4 как функция от двух исходных признаков
На следующем шаге мы рассмотрим "ядерный трюк".
