На этом шаге мы рассмотрим принципы работы SVM.
В ходе обучения SVM вычисляет важность каждой точки обучающих данных с точки зрения определения решающей границы между двумя классами. Обычно лишь часть точек обучающего набора важна для определения границы принятия решений: точки, которые лежат на границе между классами. Они называются опорными векторами (support vectors) и дали свое название машине опорных векторов.
Чтобы получить прогноз для новой точки, измеряется расстояние до каждого опорного вектора. Классификационное решение принимается, исходя из расстояний до опорных векторов, а также важности опорных векторов, полученных в процессе обучения (хранятся в атрибуте dual_coef_ класса SVC).
Расстояние между точками данных измеряется с помощью гауссовского ядра:
krbf(x1, x2) = exp(-γ|| x1 - x2||2)
Здесь x1 и x2 - точки данных, || x1 - x2|| обозначает евклидово расстояние, а γ (гамма) - параметр, который регулирует ширину гауссовского ядра.
Рисунок 1 показывает результат обучения машины опорных векторов на двумерном 2-классовом наборе данных. Граница принятия решений показана черным цветом, а опорные векторы - это точки большего размера, обведенные широким контуром. Программный код строит этот график, обучая SVM на наборе данных forge:
[In 7]: from sklearn.svm import SVC X, y = mglearn.tools.make_handcrafted_dataset() svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y) mglearn.plots.plot_2d_separator(svm, X, eps=.5) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) # размещаем на графике опорные векторы sv = svm.support_vectors_ # метки классов опорных векторов определяются знаком дуальных коэффициентов sv_labels = svm.dual_coef_.ravel() > 0 mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15, markeredgewidth=3) plt.xlabel("Признак 0") plt.ylabel("Признак 1")
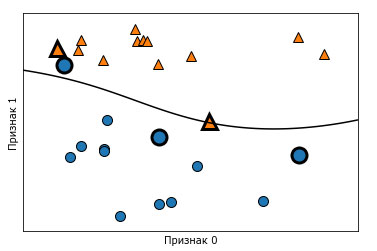
Рис.1. Граница принятия решений и опорные векторы, найденные SVM с помощью ядра RBF
В данном случае SVM дает очень гладкую и нелинейную (непрямую) границу. Здесь мы скорректировали параметр C и параметр gamma, которые сейчас подробно обсудим.
На следующем шаге мы рассмотрим настройку параметров SVM.
