На этом шаге мы рассмотрим настройку этих параметров.
Параметр gamma - это параметр формулы, приведенной на предыдущем шаге. Он регулирует ширину гауссовского ядра. Параметр gamma задает степень близости расположения точек. Параметр С представляет собой параметр регуляризации, аналогичный тому, что использовался в линейных моделях. Он ограничивает важность каждой точки (точнее, ее dual_coef_).
Давайте посмотрим, что происходит при изменении этих параметров (рисунок 1):
[In 9]: fig, axes = plt.subplots(3, 3, figsize=(15, 10)) for ax, C in zip(axes, [-1, 0, 3]): for a, gamma in zip(ax, range(-1, 2)): mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a) axes[0, 0].legend(["class 0", "class 1", "sv class 0", "sv class 1"], ncol=4, loc=(.9, 1.2))
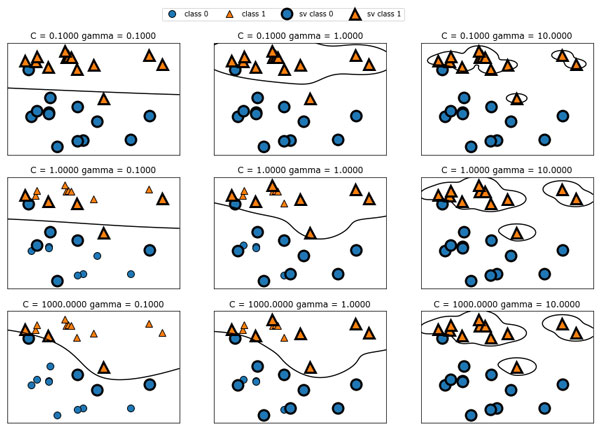
Рис.1. Границы принятия решений и опорные векторы для различных значений параметров C и gamma
Перемещаясь слева направо, мы увеличиваем значение параметра gamma c 0.1 до 10. Небольшое значение gamma соответствует большому радиусу гауссовского ядра, это означает, что многие точки рассматриваются как расположенные поблизости. Это приводит к получению очень гладких границ принятия решений, показанных в левой части графика, а границы, которые больше фокусируются на отдельных точках, расположились в правой части графика. Низкое значение gamma означает медленное изменение решающей границы, которое дает модель низкой сложности, в то время как высокое значение gamma дает более сложную модель.
Перемещаясь сверху вниз, мы увеличиваем параметр C с 0.1 до 1000. Как и в случае с линейными моделями, небольшое значение C соответствует модели с весьма жесткими ограничениями, в которой каждая точка данных может иметь лишь очень ограниченное влияние. В левом верхнем углу рисунка можно увидеть, что граница принятия решений выглядит как почти линейная, неправильно классифицированные точки почти не влияют на линию. Увеличение значения C, как показано в левом нижнем углу, позволяет этим точкам оказывать более сильное влияние на модель и делает решающую границу изогнутой, позволяя правильно классифицировать данные точки.
Давайте применим SVM c RBF-ядром к набору данных Breast Cancer. По умолчанию используются C=1 и gamma=1/n_features:
[In 10]: from sklearn.model_selection import train_test_split from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() X_train, X_test, y_train, y_test = train_test_split( cancer.data, cancer.target, random_state=0) svc = SVC() svc.fit(X_train, y_train) print("Правильность на обучающем наборе: {:.2f}". format(svc.score(X_train, y_train))) print("Правильность на тестовом наборе: {:.2f}". format(svc.score(X_test, y_test))) Правильность на обучающем наборе: 0.90 Правильность на тестовом наборе: 0.94
Хотя SVM часто дает хорошее качество модели, он очень чувствителен к настройкам параметров и масштабированию данных. В частности, SVM требует, чтобы все признаки были измерены в одном и том же масштабе. Давайте посмотрим на минимальное и максимальное значения каждого признака в log-пространстве (рисунок 2):
[In 11]: plt.plot(X_train.min(axis=0), 'o', label="min") plt.plot(X_train.max(axis=0), '^', label="max") plt.legend(loc=4) plt.xlabel("Индекс признака") plt.ylabel("Величина признака") plt.yscale("log")
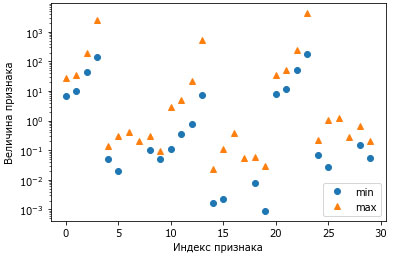
Рис.2. Диапазоны значений признаков для набора данных Breast Cancer (обратите внимание, что ось у имеет логарифмическую шкалу)
Исходя из этого графика, мы можем заключить, что признаки в наборе данных Breast Cancer имеют совершенно различные порядки величин. Для ряда моделей (например, для линейных моделей) данный факт может быть в некоторой степени проблемой, однако для ядерного SVM он будет иметь разрушительные последствия. Давайте рассмотрим некоторые способы решения этой проблемы.
На следующем шаге мы рассмотрим предварительную обработку данных для SVM.
