На этом шаге мы рассмотрим простую модель нейронной сети.
MLP можно рассматривать как обобщение линейных моделей, которое прежде чем прийти к решению выполняет несколько этапов обработки данных.
Вспомним, что в линейной регрессии прогноз получают с помощью следующей формулы:
y = w[0]* x[0] + w[1] * x[1] +... + w[p] * x[p] + b
Говоря простым языком, у - это взвешенная сумма входных признаков х[0] ... x[р]. Входные признаки взвешены по вычисленным в ходе обучения коэффициентам w[0] ... w[р]. Мы может представить их графически, как показано на рисунке 1:
[In 2]:
display(mglearn.plots.plot_logistic_regression_graph())
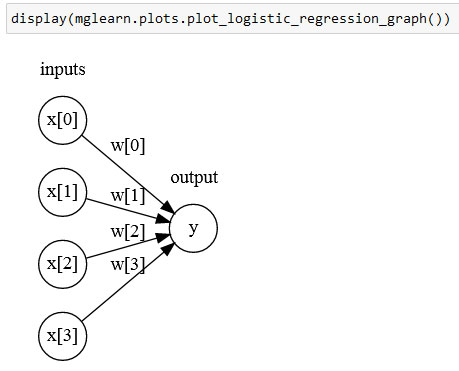
Рис.1. Визуализация логистической регрессии, в которой входные признаки и прогнозы показаны в виде узлов, а коэффициенты - в виде соединений между узлами
Здесь каждый узел, показанный слева, представляет собой входной признак, соединительные линии - коэффициенты, а узел справа - это выход, который является взвешенной суммой входов.
В MLP процесс вычисления взвешенных сумм повторяется несколько раз. Сначала вычисляются скрытые элементы (hidden units), которые представляют собой промежуточный этап обработки. Они вновь объединяются с помощью взвешенных сумм для получения конечного результата (рисунок 2):
[In 3]:
display(mglearn.plots.plot_single_hidden_layer_graph())
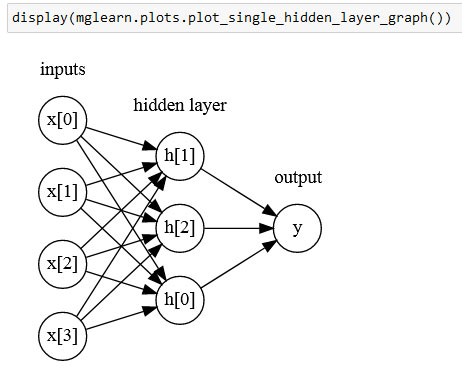
Рис.2. Иллюстрация многослойного персептрона с одним скрытым слоем
У этой модели гораздо больше вычисляемых коэффициентов (также называемых весами): коэффициент между каждым входом и каждым скрытым элементом (которые образуют скрытый слой или hidden layer) и коэффициент между каждым элементом скрытого слоя и выходом.
С математической точки зрения вычисление серии взвешенных сумм - это то же самое, что вычисление лишь одной взвешенной суммы, таким образом, чтобы эта модель обладала более мощной прогнозной силой, чем линейная модель, нам нужен один дополнительный трюк. Поясним его на примере нейронной сети с одним скрытым слоем. Входной слой просто передает входы скрытому слою сети, либо без преобразования, либо выполнив сначала стандартизацию входов. Затем происходит вычисление взвешенной суммы входов для каждого элемента скрытого слоя, к ней применяется функция активации - обычно используются нелинейные функции выпрямленный линейный элемент (rectified linear unit или relu) или гиперболический тангенс (hyperbolic tangent или tanh). В итоге получаем выходы нейронов скрытого слоя. Эти промежуточные выходы могут считаться нелинейными преобразованиями и комбинациями первоначальных входов. Они становятся входами выходного слоя. Снова вычисляем взвешенную сумму входов, применяем функцию активации и получаем итоговые значения целевой переменной. Функции активации relu и tanh показаны на рисунке 3.
[In 4]: line = np.linspace(-3, 3, 100) plt.plot(line, np.tanh(line), label="tanh") plt.plot(line, np.maximum(line, 0), label="relu") plt.legend(loc="best") plt.xlabel("x") plt.ylabel("relu(x), tanh(x)")
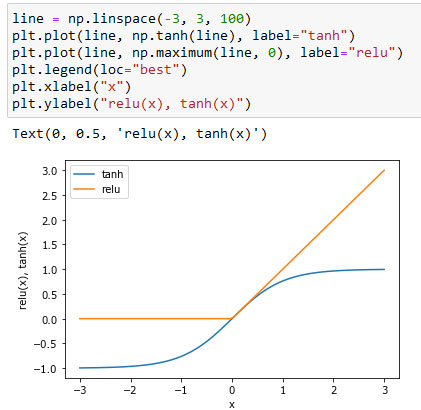
Рис.3. Функция активации гиперболический тангенс и функция активации выпрямленного линейного элемента
Relu отсекает значения ниже нуля, в то время как tanh принимает значения от -1 до 1 (соответственно для минимального и максимального значений входов). Любая из этих двух нелинейных функций позволяет нейронной сети в отличие от линеиной модели вычислять гораздо более сложные зависимости.
Для небольшой нейронной сети, изображенной на рисунке 2, полная формула вычисления у в случае регрессии будет выглядеть так (при использовании tanh):
h[0] = tanh(w[0, 0] * x[0] + w[1, 0] * x[1] + w[2, 0] * х[2] + w[3, 0] * x[3]) h[1] = tanh(w[0, 0] * x[0] + w[1, 0] * x[1] + w[2, 0] * x[2] + w[3, 0] * x[3]) h[2] = tanh(w[0, 0] * x[0] + w[1, 0] * x[1] + w[2, 0] * x[2] + w[3, 0] * x[3]) у = v[0] * h[0] + v[1] * h[1] + v[2]* h[2]
Здесь w - веса между входом х и скрытом слоем h, а v - весовые коэффициенты между скрытым слоем h и выходом у. Веса v и w вычисляются по данным, х являются входными признаками, у - вычисленный выход, а h - промежуточные вычисления. Важный параметр, который должен задать пользователь - количество узлов в скрытом слое. Его значение может быть маленьким, например, 10 для очень маленьких или простых наборов данных или же большим, например, 10000 для очень сложных данных. Кроме того, можно добавить дополнительные скрытые слои, как показано на рисунке 4:
[In 5]:
display(mglearn.plots.plot_two_hidden_layer_graph())
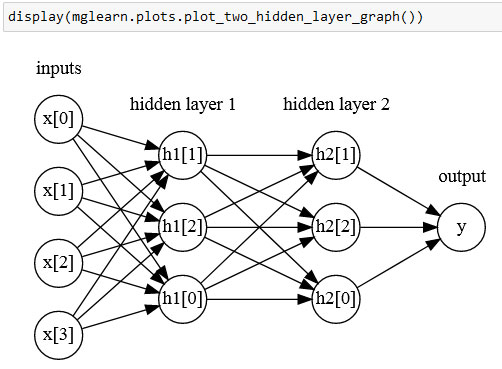
Рис.4. Многослойный персептрон с двумя скрытыми слоями
Построение больших нейронных сетей, состоящих из множества слоев вычислений, вдохновило специалистов ввести в обиход термин "глубокое обучение" ("deep learning").
На следующем шаге мы рассмотрим настройку нейронных сетей.
