На этом шаге мы рассмотрим несколько параметров, позволяющих настроить нейронную сеть.
Давайте посмотрим, как работает MLP, применив MLPClassifier к набору данных two_moons, который мы использовали ранее. Результаты показаны на рисунке 1:
[In 6]: from sklearn.neural_network import MLPClassifier from sklearn.datasets import make_moons from sklearn.model_selection import train_test_split X, y = make_moons(n_samples=100, noise=0.25, random_state=3) X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42) mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train) mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3) mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train) plt.xlabel("Признак 0") plt.ylabel("Признак 1")
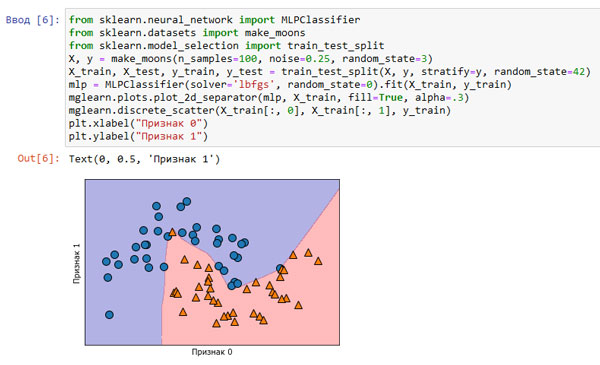
Рис.1. Граница принятия решений, построенная нейронной сетью со 100 скрытыми элементами на наборе данных two_moons
Как видно из рисунка 1, нейронная сеть построила нелинейную, но относительно гладкую границу принятия решений. Мы использовали solver='lbfgs', который рассмотрим позднее.
По умолчанию MLP использует 100 скрытых узлов, что довольно много для этого небольшого набора данных. Мы можем уменьшить число (что снизит сложность модели) и снова получить хороший результат (рисунок 2):
[In 7]: mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10]) mlp.fit(X_train, y_train) mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3) mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train) plt.xlabel("Признак 0") plt.ylabel("Признак 1")

Рис.2. Граница принятия решений, построенная нейронной сетью с 10 скрытыми элементами на наборе данных two_moons
При использовании лишь 10 скрытых элементов граница принятия решений становится более неровной. По умолчанию используется функция активации relu, показанная на рисунке 3 69 шага:
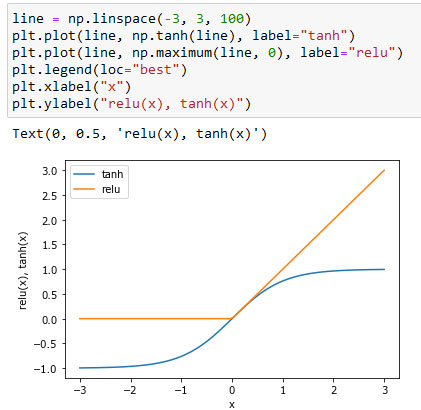
Рис.3. Рисунок 3 из 69 шага, иллюстрирующий функцию активации гиперболический тангенс и функцию активации выпрямленного линейного элемента
При использовании одного скрытого слоя решающая функция будет состоять из 10 прямолинейных отрезков. Если необходимо получить более гладкую решающую границу, можно добавить большее количество скрытых элементов (как показано на рисунке 2), добавить второй скрытый слой (рисунок 4), или использовать функцию активации tanh (рисунок 5):
[In 8]: # использование двух скрытых слоев по 10 элементов в каждом mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10, 10]) mlp.fit(X_train, y_train) mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3) mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train) plt.xlabel("Признак 0") plt.ylabel("Признак 1")

Рис.4. Граница принятия решений, построенная нейронной сетью с 2 скрытыми слоями по 10 элементов в каждом и функцией активации выпрямленный линейный элемент
# использование двух скрытых слоев по 10 элементов в каждом, на этот раз с функцией tanh [In 9]: mlp = MLPClassifier(solver='lbfgs', activation='tanh', random_state=0, hidden_layer_sizes=[10, 10]) mlp.fit(X_train, y_train) mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3) mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train) plt.xlabel("Признак 0") plt.ylabel("Признак 1")
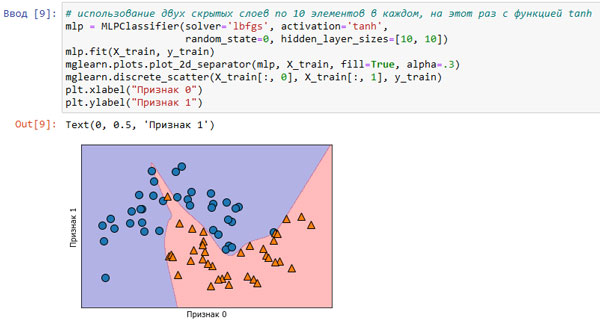
Рис.5. Граница принятия решений, построенная нейронной сетью с 2 скрытыми слоями по 10 элементов в каждом и функцией активации гиперболический тангенс
И, наконец, мы можем дополнительно настроить сложность нейронной сети с помощью l2 штрафа, чтобы сжать весовые коэффициенты до близких к нулю значений, как мы это делали в гребневой регрессии и линейных классификаторов. В MLPClassifier за это отвечает параметр alpha (как и в моделях линейной регрессии), и по умолчанию установлено очень низкое значение (небольшая регуляризация). На рисунке 6 показаны результаты применения к набору данных two_moons различных значений alpha с использованием двух скрытых слоев с 10 или 15 элементами в каждом:
[In 10]: fig, axes = plt.subplots(2, 4, figsize=(20, 8)) for axx, n_hidden_nodes in zip(axes, [10, 15]): for ax, alpha in zip(axx, [0.0001, 0.01, 0.1, 1]): mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[n_hidden_nodes, n_hidden_nodes], alpha=alpha) mlp.fit(X_train, y_train) mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax) mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax) ax.set_title("n_hidden=[{}, {}]\nalpha={:.4f}".format( n_hidden_nodes, n_hidden_nodes, alpha))
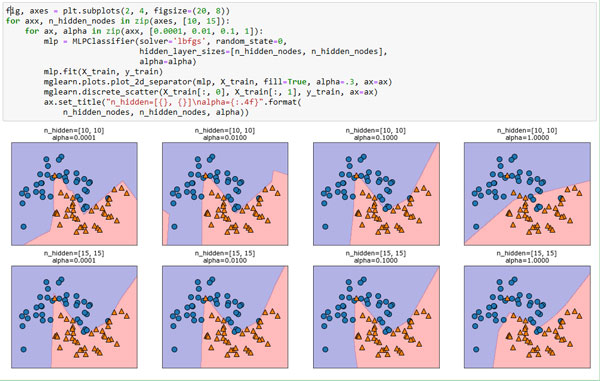
Рис.6. Границы принятия решений для различного количества скрытых элементов и разных значений параметра alpha
Как вы, наверное, уже поняли, существуют различные способы регулировать сложность нейронной сети: количество скрытых слоев, количество элементов в каждом скрытом слое и регуляризация (alpha). На самом деле их гораздо больше, но мы не будем здесь вдаваться в подробности.
Важным свойством нейронных сетей является то, что их веса задаются случайным образом перед началом обучения и случайная инициализация влияет на процесс обучения модели. Это означает, что даже при использовании одних и тех же параметров мы можем получить очень разные модели, задавая разные стартовые значения генератора псевдослучайных чисел. При условии, что сеть имеет большой размер и ее сложность настроена правильно, данный факт не должен сильно влиять на правильность, однако о нем стоит помнить (особенно при работе с небольшими сетями). На рисунке 7 представлены графики нескольких моделей, обученных с использованием тех же самых значений параметров:
[In 11]: fig, axes = plt.subplots(2, 4, figsize=(20, 8)) for i, ax in enumerate(axes.ravel()): mlp = MLPClassifier(solver='lbfgs', random_state=i, hidden_layer_sizes=[15, 15]) mlp.fit(X_train, y_train) mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax) mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax)

Рис.7. Границы принятия решений, полученные с использованием тех же самых параметров, но разных стартовых значений
На следующем шаге мы закончим изучение этого вопроса.
