На этом шаге мы рассмотрим, какие результаты можно получить, используя PCA.
Анализ главных компонент представляет собой метод, который осуществляет вращение данных с тем, чтобы преобразованные признаки не коррелировали между собой. Часто это вращение сопровождается выбором подмножества новых признаков в зависимости от их важности с точки зрения интерпретации данных. Следующий пример (рисунок 1) иллюстрирует результат применения PCA к синтетическому двумерному массиву данных:
[In 13]:
mglearn.plots.plot_pca_illustration()
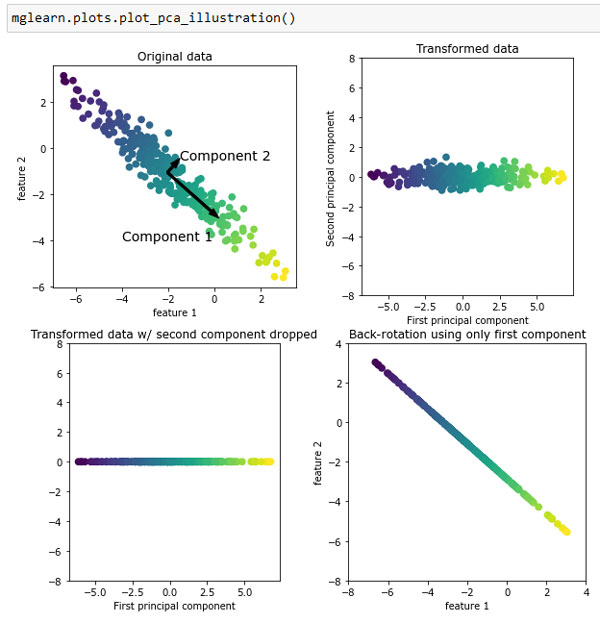
Рис.1. Преобразование данных с помощью PCA
Первый рисунок (вверху слева) показывает исходные точки данных, выделенные цветом для лучшей дискриминации. Алгоритм начинает работу с того, что сначала находит направление максимальной дисперсии, помеченное как "компонента 1". Речь идет о направлении (или векторе) данных, который содержит большую часть информации, или другими словами, направление, вдоль которого признаки коррелируют друг с другом сильнее всего. Затем алгоритм находит направление, которое содержит наибольшее количество информации, и при этом ортогонально (расположено под прямым углом) первому направлению. В двумерном пространстве существует только одна возможная ориентация, расположенная под прямым углом, но в пространствах большей размерности может быть (бесконечно) много ортогональных направлений. Хотя эти две компоненты изображаются в виде стрелок, на самом деле не имеет значения, где начало, а где конец, мы могли бы нарисовать первую компоненту, выходящую из центра в верхний левый угол, а не в нижний правый. Направления, найденные с помощью этого алгоритма, называются главными компонентами (principal components), поскольку они являются основными направлениями дисперсии данных. В целом максимально возможное количество главных компонент равно количеству исходных признаков.
Второй график (вверху справа) показывает те же самые данные, но теперь повернутые таким образом, что первая главная компонента совпадает с осью х, а вторая главная компонента совпадает с осью у. Перед вращением из каждого значения данных вычитается среднее, таким образом, преобразованные данные центрированы около нуля. В новом представлении данных, найденном с помощью PCA, две оси становятся некоррелированными. Это означает, что в новом представлении все элементы корреляционной матрицы данных, кроме диагональных, будут равны нулю.
Мы можем использовать PCA для уменьшения размерности, сохранив лишь несколько главных компонент. В данном примере мы можем оставить лишь первую главную компоненту, как показано на третьем графике рисунка 1 (внизу слева). Это уменьшит размерность данных: из двумерного массива данных получаем одномерный массив данных. Однако следует отметить, что вместо того, чтобы оставить лишь один из исходных признаков, мы находим наиболее интересное направление (выходящее из верхнего левого угла в нижний правый на первом графике) и оставляем это направление, т.е. первую главную компоненту.
И, наконец, мы можем отменить вращение и добавить обратно среднее значение к значениям данных. В итоге получим данные, показанные на последнем графике рисунка 1. Эти точки располагаются в пространстве исходных признаков, но мы оставили лишь информацию, содержащуюся в первой главной компоненте. Это преобразование иногда используется, чтобы удалить эффект шума из данных или показать, какая часть информации сохраняется при использовании главных компонент.
На следующем шаге мы рассмотрим применение РСА к набору данных cancer для визуализации.
