На этом шаге мы рассмотрим организацию таких преобразований и обсудим их применимость.
Мы только что увидели, что добавление признаков, возведенных в квадрат или куб, может улучшить линейные модели регрессии. Существуют и другие преобразования, которые часто оказываются полезными в плане трансформации определенных признаков: в частности, применение математических функций типа log(), exp() или sin(). Если модели на основе дерева заботятся лишь о выстраивании признаков в иерархию, то линейные модели и нейронные сети очень привязаны к масштабу и распределению каждого признака, поэтому наличие нелинейной взаимосвязи между признаком и зависимой переменной становится проблемой для модели, особенно для регрессии. Фунции log() и exp() позволяют скорректировать относительные шкалы переменных таким образом, чтобы линейная модель или нейронная сеть могли лучше обработать их. Мы видели подобный пример, когда работали с набором данных ram_prices. Функции sin() и cos() могут пригодиться при работе с данными, которые представляют собой периодические структуры.
Большинство моделей работают лучше, когда признаки (а если используется регрессия, то и зависимая переменная) имеют гауссовское распределение, то есть гистограмма каждого признака должна в определенной степени иметь сходство с "колоколообразной кривой". Использование преобразований типа log() и ехр() является банальным, но в то же время простым и эффективным способом добиться более симметричного распределения. Наиболее характерный случай, когда подобное преобразование может быть полезно, - обработка дискретных данных. Под дискретными данными мы подразумеваем признаки типа "как часто пользователь A входил в систему". Дискретные данные никогда не бывают отрицательными и часто подчиняются конкретным статистическим закономерностям. Здесь мы воспользуемся синтетическим набором дискретных данных с теми же самыми признаками, что можно встретить в реальной практике.
Это очень грубая аппроксимация с использованием регрессии Пуассона, которое было бы правильным решением с вероятностной точки зрения.
Все признаки имеют целочисленные значения, в то время как зависимая переменная является непрерывной:
[In 32]: rnd = np.random.RandomState(0) X_org = rnd.normal(size=(1000, 3)) w = rnd.normal(size=3) X = rnd.poisson(10 * np.exp(X_org)) y = np.dot(X_org, w)
Давайте посмотрим на первые 10 элементов первого признака. Все они являются положительными и целочисленными значениями, однако выделить какую-то определенную структуру сложно.
Если посчитать частоту встречаемости каждого значения, распределение значений становится более ясным:
[In 33]: print("Частоты значений:\n{}".format(np.bincount(X[:, 0]))) Частоты значений: [28 38 68 48 61 59 45 56 37 40 35 34 36 26 23 26 27 21 23 23 18 21 10 9 17 9 7 14 12 7 3 8 4 5 5 3 4 2 4 1 1 3 2 5 3 8 2 5 2 1 2 3 3 2 2 3 3 0 1 2 1 0 0 3 1 0 0 0 1 3 0 1 0 2 0 1 1 0 0 0 0 1 0 0 2 2 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
Значение 2, по-видимому, является наиболее распространенным, оно встречается 68 раз (bincount() всегда начинает считать с 0), а частоты более высоких значений быстро падают. Однако есть несколько очень высоких значений, например, 84 и 85, которые встречаются два раза. Мы визуализируем частоты на рисунке 1:
[In 34]: bins = np.bincount(X[:, 0]) plt.bar(range(len(bins)), bins, color='gray') plt.ylabel("Частота") plt.xlabel("Значение")
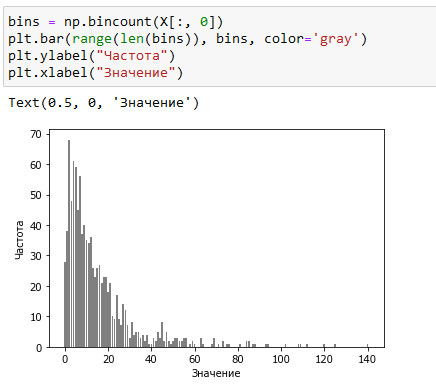
Рис.1. Гистограмма значений X[0]
Признаки X[:, 1] и X[:, 2] имеют аналогичные свойства. Полученное распределение значений (высокая частота встречаемости маленьких значений и низкая частота встречаемости больших значений) является очень распространенным явлением в реальной практике. Однако для большинства линейных моделей оно может представлять трудность. Давайте попробуем подогнать гребневую регрессию:
[In 35]: from sklearn.linear_model import Ridge X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) score = Ridge().fit(X_train, y_train).score(X_test, y_test) print("Правильность на тестовом наборе: {:.3f}".format(score)) Правильность на тестовом наборе: 0.622
Видно, что из-за относительно низкого значения R2 гребневая регрессия не может должным образом смоделировать взаимосвязь между X и у. Впрочем, применение логарифмического преобразования может помочь. Поскольку в данных появляется значение 0 (а логарифм 0 не определен), мы не можем просто взять и применить log(), вместо этого мы должны вычислить log(X + 1):
[In 36]: X_train_log = np.log(X_train + 1) X_test_log = np.log(X_test + 1)
После преобразования распределение данных стало менее асимметричным и уже не содержит очень больших выбросов (см. рисунок 2):
[In 37]: plt.hist(X_train_log[:, 0], bins=25, color='gray') plt.ylabel("Частота") plt.xlabel("Значение")
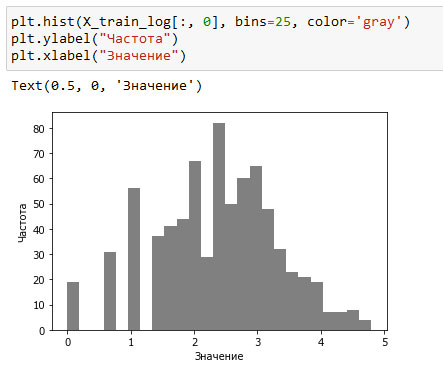
Рис.2. Гистограмма значений X[0] после логарифмического преобразования
Построение модели гребневой регрессии на новых данных дает гораздо более лучше качество подгонки:
score = Ridge().fit(X_train_log, y_train).score(X_test_log, y_test) print("Правильность на тестовом наборе: {:.3f}".format(score))
Поиск преобразования, которое наилучшим образом сработает для конкретного сочетания данных и модели - это в некоторой степени искусство. В этом примере все признаки имели одинаковые свойства. Такое редко бывает на практике, и как правило, лишь некоторые признаки нуждаются в преобразовании, либо в ряде случаев каждый признак необходимо преобразовывать по-разному. Как мы уже упоминали ранее, эти виды преобразований не имеют значения для моделей на основе дерева, но могут иметь важное значение для линейных моделей. Иногда при построении регрессии целесообразно преобразовать зависимую переменную у. Прогнозирование частот (скажем, количества заказов) является довольно распространенной задачей, и преобразование log(у + 1) часто помогает.
Как вы видели в предыдущих примерах, биннинг, полиномы и взаимодействия могут иметь огромное влияние на качество работы модели. Особенно это актуально для менее сложных моделей типа линейных моделей и наивных байесовских моделей. С другой стороны, модели на основе дерева, как правило, могут обнаружить важные взаимодействия самостоятельно и чаще всего не требуют явного преобразования данных. Использование биннинга, взаимодействий и полиномов в ряде случаев может положительно сказаться на работе моделей типа SVM, ближайших соседей и нейронных сетей, однако последствия, возникающие в результате этих преобразований, представляются менее ясными в отличие от преобразований, применяемых в линейных моделях.
На следующем шаге мы рассмотрим автоматический отбор признаков.
