На этом шаге мы рассмотрим принцип работы итеративного отбора признаков.
В одномерном отборе признаков мы не использовали модель, а в отборе признаков на основе модели мы построили одну модель, чтобы выбрать характеристики. В итеративном отборе признаков строится последовательность моделей с различным количеством признаков. Существует два основных метода. Первый метод начинается шага, когда в модель включена лишь одна константа (входных признаков нет) и затем добавляет признак за признаком до тех пор, пока не будет достигнут критерий остановки. Второй метод начинается с шага, когда все признаки включены в модель, и затем начинает удалять признак за признаком, пока не будет достигнут критерий остановки. Поскольку строится последовательность модели, эти методы с вычислительной точки зрения являются гораздо более затратными в отличие от ранее обсуждавшихся методов. Одним из таких методов является метод рекурсивного исключения признаков (recursive feature elimination, RFE), который начинается с включения всех признаков, строит модель и исключает наименее важный признак с точки зрения модели. Затем строится новая модель с использованием всех признаков, кроме исключенного, и так далее, пока не останется лишь заранее определенное количество признаков. Чтобы все получилось, модели, используемой для отбора признаков, необходима определенная метрика, измеряющая важность признаков, как было в случае с модельным отбором. Здесь мы воспользуемся той же самой моделью случайного леса, которую применяли ранее, и получим результаты, показанные на рисунке 1:
[In 46]: from sklearn.feature_selection import RFE select = RFE(RandomForestClassifier(n_estimators=100, random_state=42), n_features_to_select=40) select.fit(X_train, y_train) # визуализируем отобранные признаки: mask = select.get_support() plt.matshow(mask.reshape(1, -1), cmap='gray_r') plt.xlabel("Индекс примера")
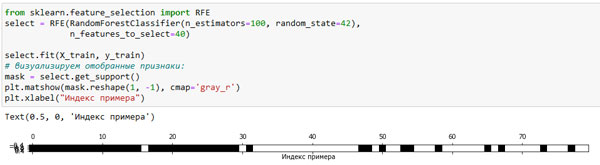
Рис.1. Признаки, отобранные методом рекурсивного исключения признаков с помощью RandomForestClassifier (изображение кликабельно)
Отбор признаков стал лучше по сравнению с одномерным отбором и отбором на основе модели, однако одного признака по-прежнему не хватает. Кроме того, выполнение этого программного кода занимает значительно больше времени в отличие от модельного отбора, поскольку модель случайного леса обучается 40 раз, по одной итерации для каждого отбрасываемого признака. Давайте проверим правильность модели логистической регрессии c использованием RFE для отбора признаков:
X_train_rfe = select.transform(X_train) X_test_rfe = select.transform(X_test) score = LogisticRegression(max_iter=600).fit(X_train_rfe, y_train).score(X_test_rfe, y_test) print("Правильность на тестовом наборе: {:.3f}".format(score)) Правильность на тестовом наборе: 0.954
Кроме того, мы можем применить модель, использованную внутри РСЕ, чтобы вычислить прогнозы. Она использует лишь набор отобранных признаков:
print("Правильность на тестовом наборе: {:.3f}".format(select.score(X_test, y_test))) Правильность на тестовом наборе: 0.951
В данном случае правильность случайного леса, используемого внутри RFE, совпадает с правильностью, достигнутой в результате обучения модели логистической регрессии на основе наилучших отобранных признаков. Другими словами, как только мы выбрали правильные признаки, линейная модель показала ту же самую правильность, что и случайный лес.
Если у вас нет уверенности в том, какие признаки использовать в качестве входных данных для вашего алгоритма машинного обучения, автоматический отбор признаков может быть весьма полезен. Кроме того, он отлично подходит для уменьшения количества необходимых признаков, например, чтобы увеличить скорость вычисления прогнозов или получить более интерпретируемые модели. В большинстве реальных примеров применение отбора признаков вряд ли обеспечит большой прирост производительности. Тем не менее, он по-прежнему является ценным инструментом в арсенале специалиста по анализу данных.
На следующем шаге мы рассмотрим применение экспертных знаний.
