На этом шаге мы рассмотрим использование этих метрик.
Теперь, когда мы подробно рассмотрели вопросы, связанные с оценкой качества бинарной классификации, давайте перейдем к метрикам для оценки качества мультиклассовой классификации. В основном, все метрики для мультиклассовой классификации являются производными от метрик классификации, но при этом усредняются по всем классам. В мультиклассовой классификации правильность вновь определяется как доля правильно классифицированных примеров. И опять же, когда классы не сбалансированы, правильность перестает быть адекватной метрикой оценки качества. Представьте себе задачу трехклассовой классификации, когда 85% точек данных принадлежат к классу А, 10% - к классу В и 5% - к классу C. Что означает среднее значение правильности 85% применительно к этому набору данных? В целом результаты мультиклассовой классификации труднее интерпретировать, чем результаты бинарной классификации. Помимо правильности часто используемыми инструментами являются матрица ошибок и отчет о результатах классификации, которые мы рассматривали, разбирая случай бинарной классификации в предыдущем разделе. Давайте применим эти два метода оценки для классификации 10 различных рукописных цифр в наборе данных digits:
[In 65]: from sklearn.metrics import accuracy_score X_train, X_test, y_train, y_test = train_test_split( digits.data, digits.target, random_state=0) lr = LogisticRegression().fit(X_train, y_train) pred = lr.predict(X_test) print("Accuracy: {:.3f}".format(accuracy_score(y_test, pred))) print("Confusion matrix:\n{}".format(confusion_matrix(y_test, pred))) Accuracy: 0.951 Confusion matrix: [[37 0 0 0 0 0 0 0 0 0] [ 0 40 0 0 0 0 0 0 2 1] [ 0 1 40 3 0 0 0 0 0 0] [ 0 0 0 43 0 0 0 0 1 1] [ 0 0 0 0 37 0 0 1 0 0] [ 0 0 0 0 0 46 0 0 0 2] [ 0 1 0 0 0 0 51 0 0 0] [ 0 0 0 1 1 0 0 46 0 0] [ 0 3 1 0 0 0 0 0 43 1] [ 0 0 0 0 0 1 0 0 1 45]]
Модель имеет точность 95.1%, что уже говорит нам об очень хорошем качестве модели. Матрица ошибок дает нам несколько более подробную информацию. Как и в случае бинарной классификации, каждая строка соответствует фактической метке класса, а каждый столбец соответствует спрогнозированной метке класса. Вы можете построить более наглядный график, приведенный на рисунке 1:
[In 66]: scores_image = mglearn.tools.heatmap( confusion_matrix(y_test, pred), xlabel='Спрогнозированная метка класса', ylabel='Фактическая метка класса', xticklabels=digits.target_names, yticklabels=digits.target_names, cmap=plt.cm.gray_r, fmt="%d") plt.title("Матрица ошибок") plt.gca().invert_yaxis()
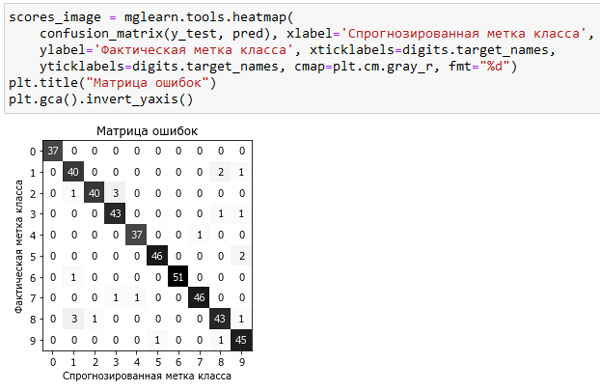
Рис.1. Матрица ошибок для десятиклассовой задачи распознавания рукописных цифр
Фактическое количество примеров, относящихся к первому классу (цифре 0), равно 37 и все эти примеры были классифицированы как класс 0 (то есть ложно отрицательные примеры для класса 0 отсутствуют). Об этом говорит тот факт, что все остальные элементы первой строки матрицы ошибок имеют нулевые значения. Кроме того, ни одна из остальных цифр не была ошибочно классифицирована как 0, поскольку все остальные элементы первого столбца имеют нулевые значения (то есть ложно положительные примеры для класса 0 отсутствуют). Однако некоторые цифры были спутаны с остальными, например, цифра 2 (третья строка), три примера, являющиеся цифрой 2, были классифицированы как цифра 3 (четвертый столбец). Кроме того, у нас есть одна цифра 3, классифицированная как 9 (десятый столбец, четвертая строка), и одна цифра 8, классифицированная как 2 (третий столбец, девятая строка).
С помощью функции classification_report() мы можем вычислить точность, полноту и 7-меру для каждого класса:
[In 67]: print(classification_report(y_test, pred)) precision recall f1-score support 0 1.00 1.00 1.00 37 1 0.89 0.93 0.91 43 2 0.98 0.91 0.94 44 3 0.91 0.96 0.93 45 4 0.97 0.97 0.97 38 5 0.98 0.96 0.97 48 6 1.00 0.98 0.99 52 7 0.98 0.96 0.97 48 8 0.91 0.90 0.91 48 9 0.90 0.96 0.93 47 accuracy 0.95 450 macro avg 0.95 0.95 0.95 450 weighted avg 0.95 0.95 0.95 450
Неудивительно, что для класса 0 получены идеальные значения точности и полноты, равные 1, поскольку все примеры классифицированы правильно. Для класса 6 получена идеальная точность, поскольку отсутствуют ложно положительные примеры (ни один из остальных классов был ошибочно классифицирован как класс 6), и для этого же класса 6 получена почти идеальная полнота, поскольку присутствует только один отсутствуют ложно отрицательный пример. Кроме того, видно, что модель испытывает ряд трудностей при классификации цифр 8 и 2.
Наиболее часто используемой метрикой для оценки качества мультиклассовой классификации для несбалансированных наборов данных является мультиклассовый вариант f1-меры. Идея, лежащая в основе мультиклассовой f1-меры, заключается в вычислении одной бинарной f1-меры для каждого класса, интересующий класс становится положительным, а все остальные - отрицательными классами. Затем эти f1-меры для каждого класса усредняются с использованием одной из следующих стратегий:
- "macro" усреднение вычисляет f1-меры для каждого класса и находит их невзвешенное среднее. Всем классам, независимо от их размера, присваивается одинаковый вес.
- "weighted" усреднение вычисляет f1-меры для каждого класса и находит их среднее, взвешенное по поддержке (количеству фактических примеров для каждого класса). Эта стратегия используется в классификационном отчете по умолчанию.
- "micro" усреднение вычисляет общее количество ложно положительных примеров, ложно отрицательных примеров и истинно положительных примеров по всем классам, а затем вычисляет точность, полноту и f1-меру с помощью этих показателей.
Если вам необходимо присвоить одинаковый вес каждому примеру, рекомендуется использовать микро-усреднение f1-меры, если вам необходимо присвоить одинаковый вес каждому классу, рекомендуется использовать макро-усреднение f1-меры:
[In 68]: print("Микро-усредненная f1-мера: {:.3f}".format (f1_score(y_test, pred, average="micro"))) print("Mакро-усредненная f1-мера: {:.3f}".format (f1_score(y_test, pred, average="macro"))) Микро-усредненная f1-мера: 0.951 Mакро-усредненная f1-мера: 0.952
На следующем шаге мы рассмотрим метрики регрессии.
