На этом шаге мы рассмотрим использование AUC.
Сравнив случайный лес и SVM с помощью AUC, мы можем сделать вывод, что случайный лес дает чуть более лучшее качество модели, чем SVM. Напомним, поскольку средняя точность - это площадь под кривой, которая принимает значения от 0 до 1, средняя точность всегда возвращает значение от 0 (худшее значение) до 1 (лучшее значение). Случайный классификатор соответствует значению AUC 0.5, независимо от того, как сбалансированы классы в наборе данных. Поэтому метрика AUC является более оптимальной, чем правильность при решении задач несбалансированной классификации. AUC можно интерпретировать как меру качества ранжирования положительных примеров. Значение площади под кривой эквивалентно вероятности того, что согласно построенной модели случайно выбранный пример положительного класса будет иметь более высокий балл, чем случайно выбранный пример отрицательного класса. Таким образом, идеальное значение AUC, равное 1, означает, что все положительные примеры в отличие от отрицательных имеют более высокий балл. В задачах несбалансированной классификации применение AUC для отбора модели зачастую является более целесообразным, чем использование правильности.
Давайте вернемся к задаче, которую мы решали ранее, классифицируя в наборе digits девятки и остальные цифры. Мы классифицируем наблюдения, используя SVM с тремя различными настройками ширины ядра и gamma (см. рисунок 1):
[In 64]: y = digits.target == 9 X_train, X_test, y_train, y_test = train_test_split( digits.data, y, random_state=0) plt.figure() for gamma in [1, 0.05, 0.01]: svc = SVC(gamma=gamma).fit(X_train, y_train) accuracy = svc.score(X_test, y_test) auc = roc_auc_score(y_test, svc.decision_function(X_test)) fpr, tpr, _ = roc_curve(y_test , svc.decision_function(X_test)) print("gamma = {:.2f} правильность = {:.2f} AUC = {:.2f}".format( gamma, accuracy, auc)) plt.plot(fpr, tpr, label="gamma={:.3f}".format(gamma)) plt.xlabel("FPR") plt.ylabel("TPR") plt.xlim(-0.01, 1) plt.ylim(0, 1.02) plt.legend(loc="best") gamma = 1.00 правильность = 0.90 AUC = 0.50 gamma = 0.05 правильность = 0.90 AUC = 1.00 gamma = 0.01 правильность = 0.90 AUC = 1.00
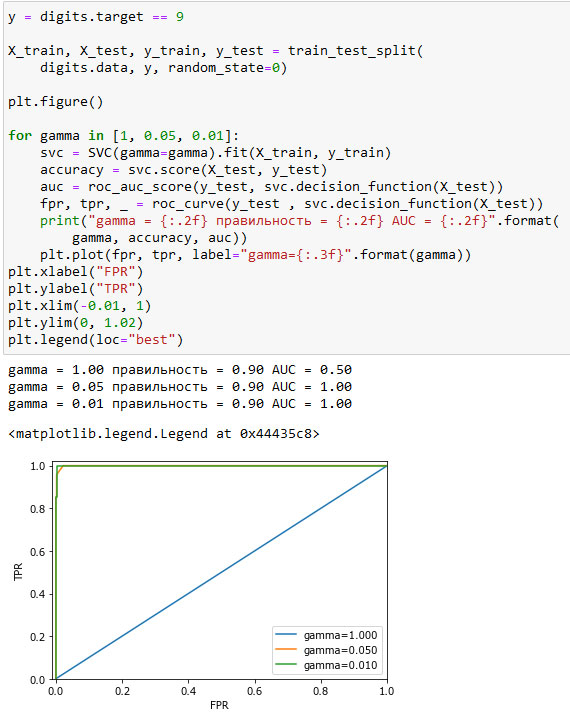
Рис.1. Сравнение ROC-кривых для SVM с различными настройками gamma
Правильность при использовании различных значений gamma остается одинаковой и составляет 90%. Одинаковое значение правильности может быть случайностью, а может быть нет. Однако взглянув на AUC и соответствующую кривую, мы видим четкое различие между этими тремя моделями. При gamma=1.0 значение AUC фактически соответствует случайному классификатору (случайному результату decision_function). При gamma=0.05 качество модели резко повышается. И, наконец, при gamma=0.01, мы получим идеальное значение AUC, равное 1.0. Это означает, что в соответствии с решающей функцией все положительные примеры получают более высокий балл, чем все отрицательные примеры. Другими словами, с помощью правильного порогового значения эта модель может идеально классифицировать данные!
Взглянув на кривую с gamma=0.01 более внимательно, вы можете увидеть небольшой излом ближе к верхнему левому углу. Это означает, что по крайней мере одна точка данных была ранжирована
неправильно. Значение AUC, равное 1.0, является результатов округления до второго знака после десятичной точки.
Зная это, мы можем скорректировать пороговое значение для этой модели и получить правильные прогнозы. Если бы мы использовали только одну точность, у нас не было бы этой информации.
По этой причине мы настоятельно рекомендуем использовать AUC для оценки качества моделей на несбалансированных данных. Однако имейте в виду, что в AUC не используется порог по умолчанию, таким образом, чтобы на основе модели с высоким значением AUC получить полезный классификатор, возможно, потребуется корректировка порогового значения.
На следующем шаге мы рассмотрим метрики для мультиклассовой классификации.
