На этом шаге мы приведем общие сведения о разработке параллельных алгоритмов для решения этой задачи.
Умножение матрицы А размера m*n и матрицы В размера n*l приводит к получению матрицы С размера m*l, каждый элемент которой определяется в соответствии с выражением:
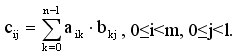
Каждый элемент результирующей матрицы С есть скалярное произведение соответствующих строки матрицы А и столбца матрицы В:
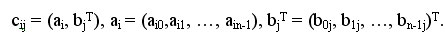
Последовательный алгоритм
Исходные данные: MatrixA[n][n], MatrixB[n][n] - исходные матрицы размерности n*n. Результат: MatrixC[n][n] - результирующая матрица.
Последовательный алгоритм умножения матриц представляется следующим образом:
for (i=0; i<Size; i++) { for (j=0; j<Size; j++) { MatrixC[i][j] = 0; for (k=0; k<Size; k++) { MatrixC[i][j]=MatrixC[i][j]+ MatrixA[i][k]*MatrixB[k][j]; } } }
Параллельные алгоритмы. Умножение матриц при ленточной схеме разделения данных
Рассмотрим два параллельных алгоритма умножения матриц, в которых матрицы A и B разбиваются на непрерывные последовательности строк или столбцов (полосы).
Для вычисления одной строки матрицы С необходимо, чтобы в каждой подзадаче содержалась строка матрицы А и был обеспечен доступ ко всем столбцам матрицы В.
1. Первый алгоритм. Алгоритм представляет собой итерационную процедуру, количество итераций которой совпадает с числом подзадач. На каждой итерации алгоритма каждая подзадача содержит по одной строке матрицы А и одному столбцу матрицы В. При выполнении итерации проводится скалярное умножение содержащихся в подзадачах строк и столбцов, что приводит к получению соответствующих элементов результирующей матрицы С. По завершении вычислений в конце каждой итерации столбцы матрицы В должны быть переданы между подзадачами с тем, чтобы в каждой подзадаче оказались новые столбцы матрицы В и могли быть вычислены новые элементы матрицы C.
2. Второй алгоритм. Отличие второго алгоритма состоит в том, что в подзадачах располагаются не столбцы, а строки матрицы B. Как результат, перемножение данных каждой подзадачи сводится не к скалярному умножению имеющихся векторов, а к их поэлементному умножению. В результате подобного умножения в каждой подзадаче получается строка частичных результатов для матрицы C.
При рассмотренном способе разделения данных для выполнения операции матричного умножения нужно обеспечить последовательное получение в подзадачах всех строк матрицы B, поэлементное умножение данных и суммирование вновь получаемых значений с ранее вычисленными результатами. Организация необходимой последовательности передач строк матрицы B между подзадачами может быть выполнена с использованием кольцевой структуры информационных связей.
На следующем шаге мы продолжим изучение этого вопроса.
