На этом шаге мы приведем некоторые положения теории графов.

Начиная с этого шага, мы рассмотрим параллельные алгоритмы, применяемые при решении некоторых задач теории графов.

Некоторые понятия теории графов

Пусть G есть граф G = (V, R), для которого набор вершин v_i, 1<=i<=n, задается множеством V, а список дуг графа r_j = (v_sj, v_tj), 1<=j<=m, определяется множеством R. В общем случае дугам графа могут приписываться некоторые числовые характеристики (веса) w_j, 1<=j<=m (взвешенный граф).

Известны различные способы задания графов. При малом количестве дуг в графе (т.е. m<<n²) целесообразно использовать для определения графов списки, перечисляющие имеющиеся в графах дуги. Представление достаточно плотных графов, для которых почти все вершины соединены между собой дугами (т.е. m~n²), может быть эффективно обеспечено при помощи матрицы смежности A = (a_ij), 1<=i, j<=n, ненулевые значения элементов которой соответствуют дугам графа

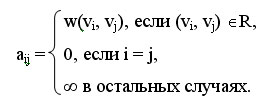
(для обозначения отсутствия ребра между вершинами в матрице смежности на соответствующей позиции используется знак бесконечности, при вычислениях знак бесконечности может быть заменен, например, на любое отрицательное число).

Использование матрицы смежности позволяет применять при реализации вычислительных процедур анализа графов матричные алгоритмы обработки данных. Далее для представления графов при рассмотрении задач будут использоваться матрицы смежности.

Задача поиска всех кратчайших путей

Исходной информацией для задачи является взвешенный граф G = (V, R), содержащий n вершин (|V| = n), в котором каждому ребру графа приписан неотрицательный вес. Граф будем полагать ориентированным, то есть если из вершины i есть ребро в вершину j, то из этого не следует наличие ребра из j в i. В случае, если вершины все же соединены взаимообратными ребрами, то веса, приписанные им, могут не совпадать. Поставим задачу нахождения путей минимальной длины между каждой парой вершин имеющегося графа G.

Задача нахождения минимального охватывающего дерева

Охватывающим деревом (или остовом) неориентированного графа G называется подграф T графа G, который является деревом и содержит все вершины из G. Определив вес подграфа для взвешенного графа как сумму весов входящих в подграф дуг, под минимально охватывающим деревом (МОД) T будем понимать охватывающее дерево минимального веса. Пример взвешенного неориентированного графа и соответствующего ему минимального охватывающего дерева приведен на рисунке 1.

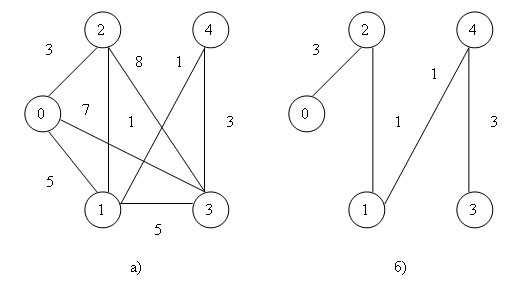
Рис.1. Пример взвешенного неориентированного графа (а) и соответствующему ему (б) минимально охватывающего дерева (б)

Задача оптимального разделения графов

Пусть дан взвешенный неориентированный граф G=(V,E), каждой вершине v, принадлежащей V, и каждому ребру e, принадлежащему E, которого приписан вес. Задача оптимального разделения графа состоит в разбиении его вершин на непересекающиеся подмножества с максимально близкими суммарными весами вершин и минимальным суммарным весом ребер, проходящих между полученными подмножествами вершин.

Следует отметить возможную противоречивость указанных критериев разбиения графа - равновесность подмножеств вершин может не соответствовать минимальности весов граничных ребер и наоборот. В большинстве случаев необходимым является выбор того или иного компромиссного решения.

Далее будем полагать веса вершин и ребер графа равными единице.

На следующем шаге мы рассмотрим последовательные алгоритмы.

Предыдущий шаг Содержание Следующий шаг