На этом шаге мы рассмотрим последовательные алгоритмы, используемые при решении задач на графах.

Последовательный алгоритм Флойда

    Для поиска минимальных расстояний между всеми парами пунктов назначения Флойд предложил алгоритм, сложность которого имеет порядок n₃. В общем виде данный алгоритм может быть представлен следующим образом:

for (k = 0; k < n; k++) 
  for (i = 0; i < n; i++)
    for (j = 0; j < n; j++)
      A[i,j] = min(A[i,j],A[i,k]+A[k,j]);

    Реализация операции выбора минимального значения min должна учитывать способ указания в матрице смежности несуществующих дуг графа. Как можно заметить, в ходе выполнения алгоритма матрица смежности A изменяется, после завершения вычислений в матрице А будет храниться требуемый результат - длины минимальных путей для каждой пары вершин исходного графа.

Последовательный алгоритм Прима

    Рассмотрим алгоритм Прима для решения задачи нахождения минимального охватывающего дерева. Алгоритм начинает работу с произвольной вершины графа, выбираемой в качестве корня дерева, и в ходе последовательно выполняемых итераций расширяет конструируемое дерево до МОД. Пусть V_T есть множество вершин, уже включенных алгоритмом в МОД, а величины d_i, 1<=i<=n, характеризуют дуги минимальной длины от вершин, еще не включенных в дерево, до множества V_T, то есть

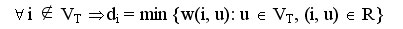
    Действия, выполняемые на каждой итерации алгоритма Прима, состоят в следующем:

1. Определяются значения величин d_i для всех вершин, еще не включенных в состав МОД.
2. Выбирается вершина t графа G, имеющая дугу минимального веса до множества V_T t: d_t = min(d_i), i не принадлежит V_T.
3. Вершина t включается в V_T.

    После выполнения n-1 итерации метода МОД будет сформировано. Вес этого дерева может быть получен при помощи выражения

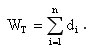
    Трудоемкость нахождения МОД характеризуется квадратичной зависимостью от числа вершин графа O(n²).

    На следующем шаге мы рассмотрим решение задачи оптимального разбиения графа.

Предыдущий шаг Содержание Следующий шаг