На этом шаге мы введем несколько новых понятий .
Дерево - это особый вид графа, в котором между любыми двумя вершинами существует один и только один путь. Это подразумевает, что в дереве нет циклов (такие графы иногда называют ациклическими). Цикл можно представить как петлю: если возможно из начальной вершины пройти по всему графу, никогда не проходя повторно ни по одному из ребер, и вернуться к начальной вершине, то в этом графе есть цикл. Любой граф, не являющийся деревом, может им стать, если удалить из него некоторые ребра. На рисунке 1 показано удаление ребер, позволяющее превратить граф в дерево.
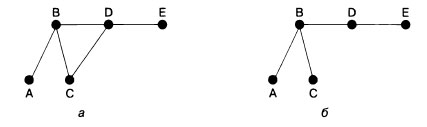
Рис.1. На левом графе существует цикл между вершинами В, С и D, поэтому он не является деревом. На правом графе ребро, соединяющее С и D, удалено, так что этот граф - дерево
Связный граф - это граф, для которого существует способ добраться из любой вершины в любую другую вершину (все графы, которые мы рассматриваем в этих шагах, являются связными). Связующее (или остовное) дерево - это дерево, которое соединяет все вершины графа. Минимальное связующее (или остовное) дерево - это дерево, которое соединяет все вершины во взвешенном графе и имеет минимальный общий вес по сравнению с другими связующими деревьями. Для каждого взвешенного графа можно найти минимальное связующее дерево.
Фууух, слишком много терминологии! Дело в том, что найти минимальное связующее дерево - это то же самое, что найти способ связать все вершины во взвешенном графе с минимальным весом. При проектировании любой сети - транспортной, компьютерной и т. д. - возникает важная практическая проблема: как с минимальными затратами подключить к сети все узлы? Этими затратами могут быть провода, трассы, дороги или что-то еще. Например, для телефонной сети другой способ постановки этой задачи таков: "Какова минимальная длина кабеля, необходимого для подключения всех телефонов?"
На следующем шаге мы поговорим об очереди с приоритетом.
