На этом шаге мы рассмотрим создание приложения, где используются эти веса.
Чтобы понять, сколько трасс может потребоваться для конкретного ребра, нам нужно знать расстояние, которое ему соответствует. Это дает возможность заново ввести понятие весов. В сети Hyperloop вес ребра - это расстояние между двумя MSA, которые оно соединяет. Рисунок 1 аналогичен рисунку 2 49 шага, за исключением того, что на нем указан вес каждого ребра, представляющий собой расстояние в милях между двумя вершинами, которые оно соединяет.
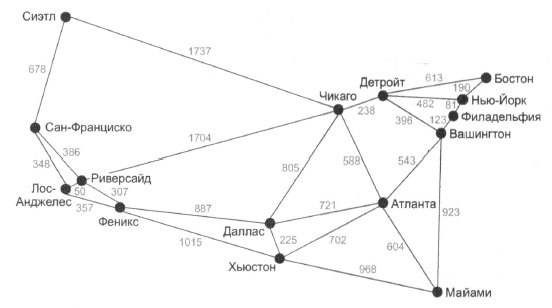
Рис.1. Взвешенный граф с 15 самыми большими MSA Соединенных Штатов, вес каждого ребра представляет собой расстояние между двумя MSA в милях
Для обработки весов понадобятся WeightedEdge (подкласс Edge) и WeightedGraph (подкласс Graph). С каждым WeightedEdge будет связано значение типа float.
Алгоритму Ярника, о котором мы вскоре расскажем, требуется возможность сравнивать ребра между собой, чтобы выбрать из них ребро с меньшим весом. Это легко реализовать посредством числовых весов (файл weighted_edge.py).
from __future__ import annotations from dataclasses import dataclass from edge import Edge @dataclass class WeightedEdge(Edge): weight: float def reversed(self) -> WeightedEdge: return WeightedEdge(self.v, self.u, self.weight) # так можно упорядочить ребра по весу и найти ребро с минимальным весом def __lt__(self, other: WeightedEdge) -> bool: return self.weight < other.weight def __str__(self) -> str: return f"{self.u} {self.weight}> {self.v}"
Реализация WeightedEdge не сильно отличается от Edge. Разница только в том, что добавлено свойство weight и оператор < реализован с помощью __lt__(), благодаря чему два объекта WeightedEdge можно сравнивать. Оператор < просматривает только веса ребер, а не унаследованные свойства u и v, так как алгоритм Ярника занимается поиском наименьшего по весу ребра.
Класс WeightedGraph наследует большую часть своей функциональности от Graph. Помимо этого, у данного класса есть методы инициализации и удобные методы сложения объектов WeightedEdge. К тому же в нем реализована собственная версия __str__(). Появился также новый метод neighbors_for_index_with_weights(), который возвращает не только все соседние вершины, но и веса ведущих к ним ребер. Этот метод будет полезен в новой версии __str__().
from typing import TypeVar, Generic, List, Tuple from pr51_1 import Graph from weighted_edge import WeightedEdge V = TypeVar('V') # тип вершин в графе class WeightedGraph(Generic[V], Graph[V]): def __init__(self, vertices: List[V] = []) -> None: self._vertices: List[V] = vertices self._edges: List[List[WeightedEdge]] = [[] for _ in vertices] def add_edge_by_indices(self, u: int, v: int, weight: float) -> None: edge: WeightedEdge = WeightedEdge(u, v, weight) self.add_edge(edge) # вызываем версию суперкласса def add_edge_by_vertices(self, first: V, second: V, weight: float) -> None: u: int = self._vertices.index(first) v: int = self._vertices.index(second) self.add_edge_by_indices(u, v, weight) def neighbors_for_index_with_weights(self, index: int) -> List[Tuple[V, float]]: distance_tuples: List[Tuple[V, float]] = [] for edge in self.edges_for_index(index): distance_tuples.append((self.vertex_at(edge.v), edge.weight)) return distance_tuples def __str__(self) -> str: desc: str = "" for i in range(self.vertex_count): desc += f"{self.vertex_at(i)} -> {self.neighbors_for_index_with_weights(i)}\n" return desc
Теперь можно наконец определить взвешенный граф. Взвешенный граф, с которым мы будем работать (см. рисунок 1), называется city_graph2.
if __name__ == "__main__": city_graph2: WeightedGraph[str] = WeightedGraph(["Сиэтл", "Сан-Франциско", "Лос-Анджелес", "Риверсайд", "Феникс", "Чикаго", "Бостон", "Нью-Йорк", "Атланта", "Майами", "Даллас", "Хьюстон", "Детройт", "Филадельфия", "Вашингтон"]) city_graph2.add_edge_by_vertices("Сиэтл", "Чикаго", 1737) city_graph2.add_edge_by_vertices("Сиэтл", "Сан-Франциско", 678) city_graph2.add_edge_by_vertices("Сан-Франциско", "Риверсайд", 386) city_graph2.add_edge_by_vertices("Сан-Франциско", "Лос-Анджелес", 348) city_graph2.add_edge_by_vertices("Лос-Анджелес", "Риверсайд", 50) city_graph2.add_edge_by_vertices("Лос-Анджелес", "Феникс", 357) city_graph2.add_edge_by_vertices("Риверсайд", "Феникс", 307) city_graph2.add_edge_by_vertices("Риверсайд", "Чикаго", 1704) city_graph2.add_edge_by_vertices("Феникс", "Даллас", 887) city_graph2.add_edge_by_vertices("Феникс", "Хьюстон", 1015) city_graph2.add_edge_by_vertices("Даллас", "Чикаго", 805) city_graph2.add_edge_by_vertices("Даллас", "Атланта", 721) city_graph2.add_edge_by_vertices("Даллас", "Хьюстон", 225) city_graph2.add_edge_by_vertices("Хьюстон", "Атланта", 702) city_graph2.add_edge_by_vertices("Хьюстон", "Майами", 968) city_graph2.add_edge_by_vertices("Атланта", "Чикаго", 588) city_graph2.add_edge_by_vertices("Атланта", "Вашингтон", 543) city_graph2.add_edge_by_vertices("Атланта", "Майами", 604) city_graph2.add_edge_by_vertices("Майами", "Вашингтон", 923) city_graph2.add_edge_by_vertices("Чикаго", "Детройт", 238) city_graph2.add_edge_by_vertices("Детройт", "Бостон", 613) city_graph2.add_edge_by_vertices("Детройт", "Вашингтон", 396) city_graph2.add_edge_by_vertices("Детройт", "Нью-Йорк", 482) city_graph2.add_edge_by_vertices("Бостон", "Нью-Йорк", 190) city_graph2.add_edge_by_vertices("Нью-Йорк", "Филадельфия", 81) city_graph2.add_edge_by_vertices("Филадельфия", "Вашингтон", 123) print(city_graph2)
Поскольку в WeightedGraph реализован метод __str__(), мы можем структурно распечатать city_graph2. При выводе вы увидите и вершины, с которыми соединена данная вершина, и веса этих соединений:
Сиэтл -> [('Чикаго', 1737), ('Сан-Франциско', 678)]
Сан-Франциско -> [('Сиэтл', 678), ('Риверсайд', 386), ('Лос-Анджелес', 348)]
Лос-Анджелес -> [('Сан-Франциско', 348), ('Риверсайд', 50), ('Феникс', 357)]
Риверсайд -> [('Сан-Франциско', 386), ('Лос-Анджелес', 50), ('Феникс', 307), ('Чикаго', 1704)]
Феникс -> [('Лос-Анджелес', 357), ('Риверсайд', 307), ('Даллас', 887), ('Хьюстон', 1015)]
Чикаго -> [('Сиэтл', 1737), ('Риверсайд', 1704), ('Даллас', 805), ('Атланта', 588),
('Детройт', 238)]
Бостон -> [('Детройт', 613), ('Нью-Йорк', 190)]
Нью-Йорк -> [('Детройт', 482), ('Бостон', 190), ('Филадельфия', 81)]
Атланта -> [('Даллас', 721), ('Хьюстон', 702), ('Чикаго', 588), ('Вашингтон', 543),
('Майами', 604)]
Майами -> [('Хьюстон', 968), ('Атланта', 604), ('Вашингтон', 923)]
Даллас -> [('Феникс', 887), ('Чикаго', 805), ('Атланта', 721), ('Хьюстон', 225)]
Хьюстон -> [('Феникс', 1015), ('Даллас', 225), ('Атланта', 702), ('Майами', 968)]
Детройт -> [('Чикаго', 238), ('Бостон', 613), ('Вашингтон', 396), ('Нью-Йорк', 482)]
Филадельфия -> [('Нью-Йорк', 81), ('Вашингтон', 123)]
Вашингтон -> [('Атланта', 543), ('Майами', 923), ('Детройт', 396), ('Филадельфия', 123)]
На следующем шаге мы рассмотрим поиск минимального связующего дерева.
