На этом шаге мы проиллюстрируем этот принцип.
Теперь вы понимаете, что суть машинного обучения заключается в преобразовании ввода (изображений) в результат путем исследования множества примеров входных данных и результатов. Вы также знаете, что глубокие нейронные сети выполняют при этом длинную последовательность простых преобразований (слоев) и обучаются этим преобразованиям на примерах. Давайте посмотрим, как именно проходит обучение.
То, что именно слой делает со своими входными данными, определяется его весами, которые фактически являются набором чисел. Выражаясь техническим языком, преобразование, реализуемое слоем, параметризуется весами (рисунок 1).
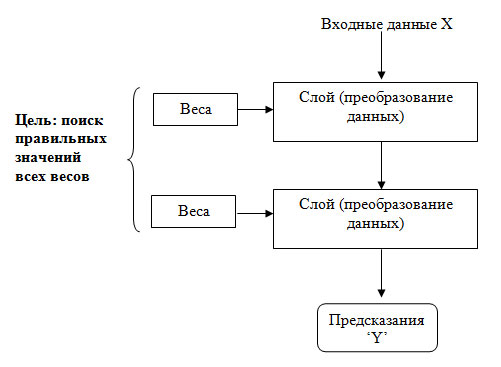
Рис.1. Нейронная сеть параметризуется ее весами
(Веса также иногда называют параметрами слоя.) В данном контексте обучение - это поиск набора значений весов всех слоев в сети, при котором сеть будет правильно отображать образцы входных данных в соответствующие им результаты. Но вот в чем дело: глубокая нейронная сеть может иметь десятки миллионов параметров. Поиск правильного значения для каждого из них может оказаться сложнейшей задачей, особенно если изменение значения одного параметра влияет на поведение всех остальных!
Чтобы чем-то управлять, сначала нужно получить возможность наблюдать за этим. Чтобы управлять результатом работы нейронной сети, нужно измерить, насколько он далек от ожидаемого. Эту задачу решает функция потерь сети, называемая также целевой функцией или функцией стоимости. Функция потерь принимает предсказание, выданное сетью, и истинное значение (которое сеть должна была вернуть) и вычисляет оценку расстояния между ними, отражающую, насколько хорошо сеть справилась с данным конкретным примером (рисунок 2).
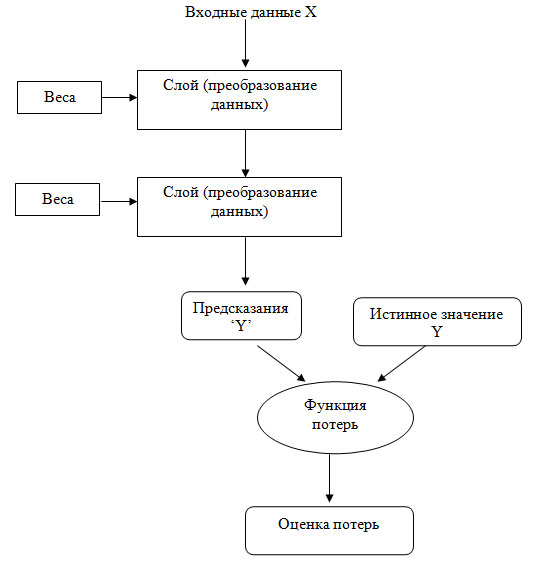
Рис.2. Функция потерь оценивает качество результатов, производимых нейронной сетью
Основная хитрость глубокого обучения заключается в использовании этой оценки для корректировки значения весов с целью уменьшения потерь в текущем примере (рисунок 3).
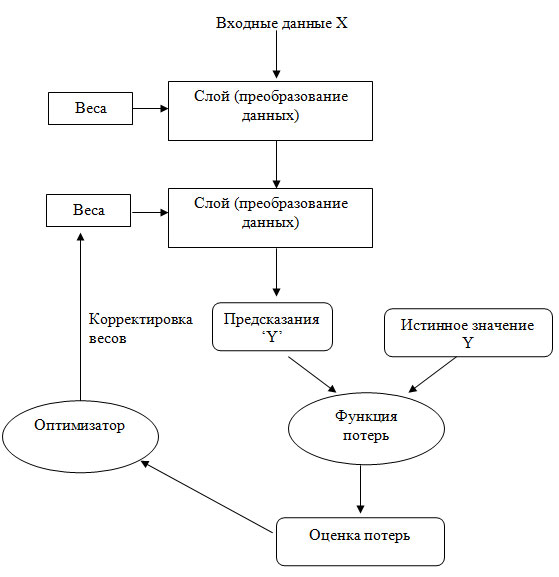
Рис.3. Оценка потерь используется как обратная связь для корректировки весов
Данная корректировка является задачей оптимизатора, который реализует так называемый алгоритм обратного распространения ошибки - центральный алгоритм глубокого обучения. Подробнее об алгоритме обратного распространения ошибки будет рассказано в следующих шагах.
Первоначально весам сети присваиваются случайные значения, то есть фактически сеть реализует последовательность случайных преобразований. Естественно, получаемый ею результат далек от идеала, и оценка потерь при этом очень высока. Но с каждым примером, обрабатываемым сетью, веса корректируются в нужном направлении и оценка потерь уменьшается. Это цикл обучения, который повторяется достаточное количество раз (обычно десятки итераций с тысячами примеров) и порождает весовые значения, минимизирующие функцию потерь. Сеть с минимальными потерями, возвращающая результаты, близкие к истинным, называется обученной сетью. Повторим еще раз: это простой механизм, который в определенном масштабе начинает выглядеть непонятным и таинственным
На следующем шаге мы рассмотрим современное состояние глубокого обучения.
