На этом шаге мы рассмотрим особенности выполнения этой операции.
Скалярное произведение, также иногда называемое тензорным произведением (не путайте с поэлементным произведением, оператором *), - наиболее общая и наиболее полезная операция с тензорами.
Поэлементное произведение в NumPy выполняется с помощью функции np.dot:
x = np.random.random((32,)) y = np.random.random((32,)) z = np.dot(x, y)
В математике скалярное произведение обозначается точкой (·):
z = x · y
Что же делает операция скалярного произведения? Для начала разберемся со скалярным произведением двух векторов, x и у:
def naive_vector_dot(x, y): # Убедиться что x, y — векторы NumPy assert len(x.shape) == 1 assert len(y.shape) == 1 assert x.shape[0] == y.shape[0] z = 0. for i in range(x.shape[0]): z += x[i] * y[i] return z
Обратите внимание, что в результате скалярного произведения двух векторов получается скаляр и в операции могут участвовать только векторы с одинаковым количеством элементов.
Также есть возможность получить скалярное произведение матрицы x на вектор y, являющееся вектором, элементы которого - скалярные произведения строк x на y. Вот как реализуется эта операция:
import numpy as np def naive_matrix_vector_dot(x, y): assert len(x.shape) == 2 # Убедиться что x — матрица NumPy assert len(y.shape) == 1 # Убедиться что y — вектор NumPy # Первое измерение x должно совпадать с нулевым измерением y! assert x.shape[1] == y.shape[0] # Эта операция вернет вектор с нулевыми элементами, имеющий ту же форму, что и y z = np.zeros(x.shape[0]) for i in range(x.shape[0]): for j in range(x.shape[1]): z[i] += x[i, j] * y[j] return z
Эта операция вернет вектор с нулевыми элементами, имеющий ту же форму, что и y.
Также можно было бы повторно использовать код, написанный прежде, подчеркнув общность произведений матрицы на вектор и вектора на вектор:
def naive_matrix_vector_dot(x, y): z = np.zeros(x.shape[0]) for i in range(x.shape[0]): z[i] = naive_vector_dot(x[i, :], y) return z
Обратите внимание, что если один из двух тензоров имеет ndim больше 1, скалярное произведение перестает быть симметричной операцией, то есть результат dot(x, y) не совпадает с результатом dot(y, x).
Разумеется, скалярное произведение можно распространить на тензоры с произвольным количеством осей. Наиболее часто на практике применяется скалярное произведение двух матриц. Получить скалярное произведение двух матриц x и y (dot(x, y)) можно, только если x.shape[1] == y.shape[0]. В результате получится матрица с формой (x.shape[0], y.shape[1]), элементами которой являются скалярные произведения строк x на столбцы y. Вот как могла бы выглядеть простейшая реализация:
def naive_matrix_dot(x, y): assert len(x.shape) == 2 # Убедиться что x, y — матрицы NumPy assert len(y.shape) == 2 # Первое измерение x должно совпадать с нулевым измерением y! assert x.shape[1] == y.shape[0] # Эта операция вернет матрицу заданной формы с нулевыми элементами z = np.zeros((x.shape[0], y.shape[1])) for i in range(x.shape[0]): # Обход строк в x... for j in range(y.shape[1]): # ...и столбцов в y row_x = x[i, :] column_y = y[:, j] z[i, j] = naive_vector_dot(row_x, column_y) return z
Эта операция вернет матрицу заданной формы с нулевыми элементами.
Чтобы было понятнее, как определяется совместимость форм матриц для скалярного произведения, представьте входные и выходной тензоры, как показано на рисунке 1.
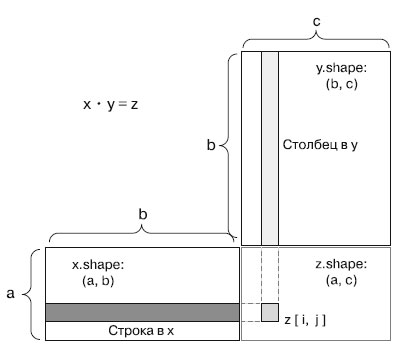
Рис.1. Диаграмма скалярного произведения матриц
Переменные x, y и z изображены здесь в виде прямоугольников (буквально - таблиц элементов). Число строк в x и столбцов в y должно совпадать, соответственно, ширина x должна равняться высоте y.
В общем случае скалярное произведение тензоров с большим числом измерений выполняется в соответствии с теми же правилами совместимости форм, как описывалось выше для случая двумерных матриц:
(a, b, c, d) · (d,) → (a, b, c) (a, b, c, d) · (d, e) → (a, b, c, e)
На следующем шаге мы рассмотрим изменение формы тензора.
