На этом шаге мы рассмотрим, как геометрически можно представить результаты операций с тензорами.

    Поскольку содержимое тензоров можно интерпретировать как координаты точек в некотором геометрическом пространстве, все операции с тензорами имеют геометрическую интерпретацию. Возьмем для примера операцию сложения. Пусть имеется следующий вектор:

A = [0.5, 1]

    Он определяет направление в двумерном пространстве (рисунок 1).

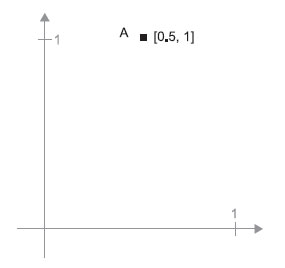
Рис.1. Точка в двумерном пространстве

    Векторы принято изображать в виде стрелок, соединяющих начало координат с заданной точкой, как показано на рисунке 2.

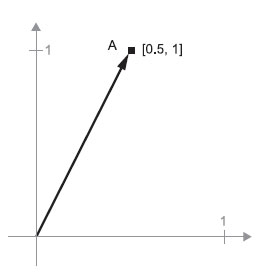
Рис.2. Вектор в двумерном пространстве, изображенный в виде стрелки

    Добавим новый вектор B = [1, 0.25] и сложим его с предыдущим. Чтобы получить результирующий вектор, представляющий сумму двух исходных векторов, достаточно перенести начало одного вектора в конец другого (рисунок 3).

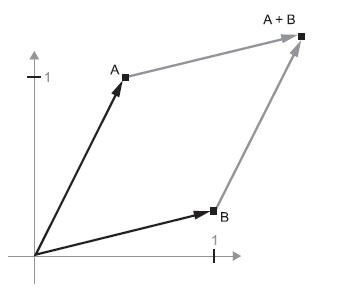
Рис.3. Геометрическая интерпретация суммы двух векторов

    Как видите, операция прибавления вектора B к вектору A заключается в переносе точки A в новое место, при этом расстояние и направление переноса от исходной точки A определяется вектором B. Если применить ту же операцию к группе точек на плоскости ("объекту"), можно создать копию целого объекта в новом месте (рисунок 4).

Рис.4. Сложение векторов как параллельный перенос в двумерном пространстве

    То есть тензорное сложение представляет операцию параллельного переноса объекта (без его искажения) на определенное расстояние в определенном направлении.

    Элементарные геометрические операции, такие как параллельный перенос, поворот, масштабирование, наклон и т. д., можно выразить в виде операций с тензорами. Вот несколько примеров:

• параллельный перенос: как показано выше, добавление вектора к точке переместит ее на фиксированное расстояние в фиксированном направлении; при применении к набору точек (например, к двумерному объекту) эта операция называется параллельным переносом (рисунок 4);

• поворот: поворот двумерного вектора на угол theta против часовой стрелки (рисунок 5) выражается как скалярное произведение с матрицей R = [u, v] размером 2 × 2, R = [[cos(theta), -sin(theta)], [sin(theta), cos(theta)]];

  
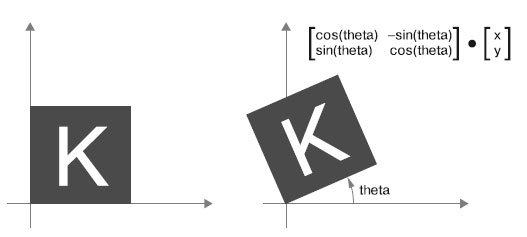
  Рис.5. Поворот двумерного вектора (против часовой стрелки) как скалярное произведение

• масштабирование: масштабирование изображения по вертикали и горизонтали (рисунок 6) можно осуществить с помощью скалярного произведения с матрицей 2 × 2, S = [[масштаб_по_горизонтали, 0], [0, масштаб_по_вертикали]] (обратите внимание, что такие матрицы называются диагональными, поскольку имеют ненулевые коэффициенты только на главной диагонали, идущей от верхнего левого угла к нижнему правому);

  
  Рис.6. Двумерное масштабирование как скалярное произведение

• линейное преобразование: скалярное произведение с произвольной матрицей реализует линейное преобразование. Обратите внимание, что масштабирование и поворот, перечисленные выше, по определению являются линейными преобразованиями;

• аффинное преобразование: аффинное преобразование (рисунок 7) - это комбинация линейного преобразования (путем скалярного произведения с некоторой матрицей) и параллельного переноса (путем сложения векторов) Как вы, наверное, уже заметили, именно это преобразование, y = W · x + b, реализует слой Dense! Полносвязанный слой Dense без функции активации является аффинным слоем;

  
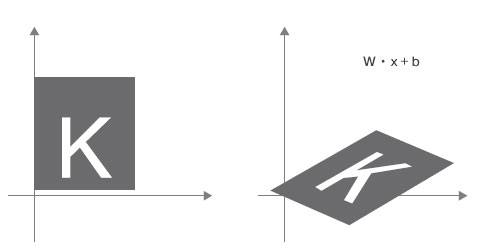
  Рис.7. Аффинное преобразование на плоскости

• полносвязанный слой (Dense) с активацией relu: аффинные преобразования обладают одним важным свойством - при многократном их применении в результате все равно получается аффинное преобразование (то есть можно сразу взять одно это суммирующее преобразование). Рассмотрим пример с двумя аффинными преобразованиями:

  affine2(affine1(x)) = W2 · (W1 · x + b1) + b2 = (W2 · W1) · x + (W2 · b1 + b2). 
  

  Это аффинное преобразование, в котором линейная часть представлена матрицей W2 · W1, а часть, отвечающая за параллельный перенос, - это вектор W2 · b1 + b2. Как следствие, многослойная нейронная сеть, полностью состоящая из слоев Dense без активаций, будет эквивалентна одному слою Dense. Значит, данная "глубокая" нейронная сеть является всего лишь замаскированной линейной моделью! Вот почему нужны функции активации, такие как relu (ее действие показано на рисунке 8).

  
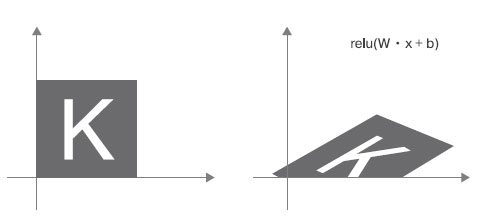
  Рис.8. Аффинное преобразование с последующим применением функции активации relu

      Благодаря им можно создать цепочку слоев Dense для реализации очень сложных нелинейных геометрических преобразований и получить богатое пространство гипотез для глубоких нейронных сетей. Эту идею мы подробно рассмотрим в следующих шагах.

    На следующем шаге мы рассмотрим геометрическую интерпретацию глубокого обучения.

Предыдущий шаг Содержание Следующий шаг