На этом шаге мы рассмотрим, что из себя представляет производная.
Рассмотрим непрерывную гладкую функцию f(x) = у, отображающую число x в новое число у. Возьмем для примера функцию, изображенную на рисунке 1.
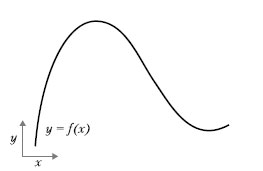
Рис.1. Непрерывная гладкая функция
Поскольку функция непрерывна, небольшое изменение x может дать в результате только небольшое изменение у - это вытекает из понятия непрерывности. Допустим, вы увеличили x на маленькую величину epsilon_x: в результате у изменилось на маленькую величину epsilon_y, как показано на рисунке 2.
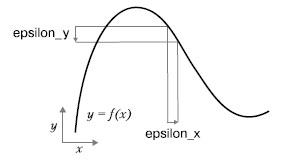
Рис.2. Для непрерывной функции небольшое изменение x даст в результате небольшое изменение y
Кроме того, поскольку функция является гладкой (ее кривая не имеет острых углов), то при малых величинах epsilon_x в окрестностях определенной точки p функцию f можно аппроксимировать линейной функцией c наклоном а. Соответственно, epsilon_y можно вычислить как а * epsilon_x:
f(x + epsilon_x) = у + а * epsilon_x
Очевидно, что такая линейная аппроксимация действительна, только когда x располагается достаточно близко к точке p.
Наклон а называется производной f в точке p. Если а имеет отрицательное значение, небольшое изменение x в окрестностях p приведет к уменьшению f(x) (как показано на рисунке 3); а если положительное - небольшое изменение x приведет к увеличению f(x).
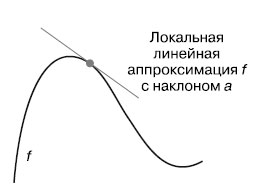
Рис.3. Производная f в точке p
Кроме того, абсолютное значение а (величина производной) сообщает, насколько большим будет это увеличение или уменьшение.
Для любой дифференцируемой функции f(x) (под дифференцируемой подразумевается "имеющей производную": например, гладкие непрерывные функции могут иметь производную) существует такая производная функция f'(x), которая отображает значения x в наклон локальной линейной аппроксимации f в этих точках. Например, производной от cos(x) является -sin(x), производной от f(x) = a * x будет f'(x) = a и т. д.
Возможность получения производной функции - очень мощный инструмент, особенно для оптимизации задачи поиска значений x, минимизирующих значение f(x). Если вы пытаетесь изменить x на величину epsilon_x, чтобы минимизировать f(x), и знаете производную от f, можете считать, что эту задачу вы уже решили: производная полностью описывает поведение f(x) с изменением x. Чтобы уменьшить значение f(x), достаточно сместить x в направлении, противоположном производной.
На следующем шаге мы рассмотрим производную операций с тензорами.
