На этом шаге мы рассмотрим, что из себя представляет стохастический градиентный спуск.
По идее, минимум дифференцируемой функции можно найти аналитически. Как известно, минимум функции - это точка, где производная равна 0. То есть остается только найти все точки, где производная обращается в 0, и выяснить, в какой из этих точек функция имеет наименьшее значение.
Применительно к нейронным сетям это означает аналитический поиск комбинации значений весов, при которых функция потерь будет иметь наименьшее значение. Добиться подобного можно, решив уравнение grad(f(W), W) = 0 для W. Это полиномиальное уравнение с N переменными, где N - число весов в модели. Решить его для случая N = 2 или N = 3 не составляет труда, но для нейронных сетей, где число параметров редко бывает меньше нескольких тысяч, а часто достигает вообще нескольких десятков миллионов, - это практически неразрешимая задача
Поэтому на практике используется алгоритм из четырех шагов, представленный на 47 шаге. Параметры изменяются на небольшую величину, исходя из текущих значений потерь в случайном пакете данных. Поскольку функция дифференцируема, можно вычислить ее градиент, который позволяет эффективно реализовать шаг 4. Если веса изменить в направлении, противоположном градиенту, потери с каждым циклом будут понемногу уменьшаться.
- Извлекается пакет обучающих экземпляров x и соответствующих целей y_true.
- Модель обрабатывает пакет x и получает пакет предсказаний y_pred.
- Вычисляются потери модели на пакете, дающие оценку несовпадения между y_pred и y_true.
- Вычисляется градиент потерь для весов модели (обратный проход). Веса модели корректируются на небольшую величину в направлении, противоположном градиенту (например, W -= скорость_обучения * градиент), и тем самым снижаются потери. Скорость обучения - скалярный множитель, модулирующий "скорость" процесса градиентного спуска.
Выглядит довольно просто! Мы только что описали стохастический градиентный спуск на небольших пакетах (mini-batch stochastic gradient descent, mini-batch SGD). Термин "стохастический" отражает тот факт, что каждый пакет данных выбирается случайно (в науке слово "стохастический" считается синонимом слова "случайный"). Рисунок 1 иллюстрирует происходящее на примере одномерных данных, когда модель имеет только один параметр и в вашем распоряжении есть только один обучающий образец.
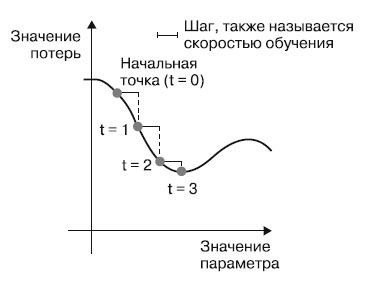
Рис.1. Стохастический градиентный спуск вниз по одномерной кривой потерь (один обучаемый параметр)
Как можно заметить, выбор разумной величины скорости обучения имеет большое значение. Если взять ее слишком маленькой, спуск потребует большого количества итераций и может застрять в локальном минимуме. Если слишком большой - корректировки могут в конечном счете привести в абсолютно случайные точки на кривой.
Обратите внимание, что вариант алгоритма mini-batch SGD в каждой итерации использует единственный образец и цель, а не весь пакет данных. Фактически это истинный SGD (а не mini-batch SGD). Однако можно пойти другим путем и использовать на каждом шаге все доступные данные. Эта версия алгоритма называется пакетным градиентным спуском (batch gradient descent). Каждое изменение в этом случае будет более точным, но более затратным. Эффективным компромиссом между этими двумя крайностями является использование пакетов умеренного размера.
На рисунке 1 изображен градиентный спуск в одномерном пространстве параметров, но на практике чаще используется градиентный спуск в пространствах с намного большим числом измерений: каждый весовой коэффициент в нейронной сети - это независимое измерение в пространстве, и их может быть десятки тысяч или даже миллионы. Чтобы лучше понять поверхности потерь, представьте градиентный спуск по двумерной поверхности, как показано на рисунке 2.
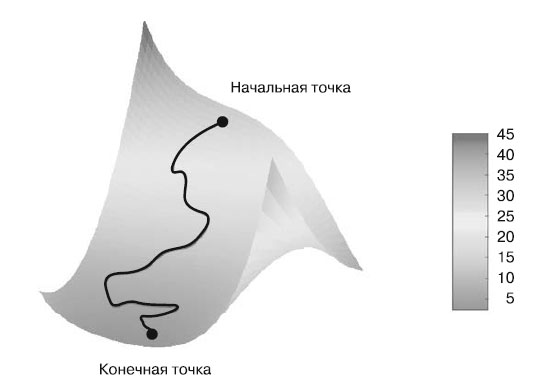
Рис.2. Градиентный спуск вниз по двумерной поверхности потерь (два обучаемых параметра)
Но имейте в виду, что вам не удастся мысленно визуализировать фактический процесс обучения нейронной сети - с 1 000 000-мерным пространством этого не получится. Поэтому всегда помните, что представление, полученное на таких моделях с небольшим числом измерений, на практике может быть не всегда точным. В прошлом это часто приводило к ошибкам исследователей глубокого обучения.
Существует также множество вариантов стохастического градиентного спуска, которые отличаются тем, что при вычислении следующих приращений весов принимают в учет не только текущие значения градиентов, но и предыдущие приращения. Примерами могут служить такие алгоритмы, как SGD с импульсом, Adagrad, RMSProp и некоторые другие. Эти варианты известны как методы оптимизации, или оптимизаторы. В частности, внимания заслуживает идея импульса, которая используется во многих подобных вариантах. Импульс вводится для решения двух проблем SGD:
- невысокой скорости сходимости и
- попадания в локальный минимум.
Взгляните на рисунок 3, на котором изображена кривая потерь как функция параметра сети.
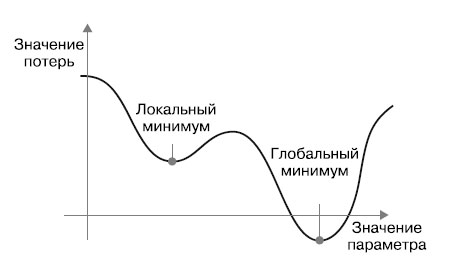
Рис.3. Локальный и глобальный минимумы
Как видите, для значения данного параметра имеется локальный минимум: движение из этой точки влево или вправо повлечет увеличение потери. Если корректировка рассматриваемого параметра осуществляется методом градиентного спуска с маленькой скоростью обучения, процесс оптимизации может застрять в локальном минимуме, не найдя пути к глобальному минимуму.
Таких проблем можно избежать, если использовать идею импульса, заимствованную из физики. Вообразите, что процесс оптимизации - это маленький шарик, катящийся вниз по кривой потерь. Если шарик имеет достаточно высокий импульс, он не застрянет в мелком овраге и окажется в глобальном минимуме. Импульс реализуется путем перемещения шарика на каждом шаге исходя не только из текущей величины наклона (текущего ускорения), но и из текущей скорости (набранной в результате действия силы ускорения на предыдущем шаге). На практике это означает, что приращение параметра w определяется не только по текущему значению градиента, но и по величине предыдущего приращения параметра, как показано в следующей упрощенной реализации:
past_velocity = 0. momentum = 0.1 # Постоянное значение импульса while loss > 0.01: # Цикл оптимизации w, loss, gradient = get_current_parameters() velocity = past_velocity * momentum - learning_rate * gradient w = w + momentum * velocity - learning_rate * gradient past_velocity = velocity update_parameter(w)
Со следующего шага мы начнем знакомиться с алгоритмом обратного распространения ошибки.
