На этом шаге мы рассмотрим пример использования графа вычислений.
Обратное распространение можно представить в виде графа вычислений. Граф вычислений - это структура данных, лежащая в основе TensorFlow и давшая начало революции глубокого обучения в целом. Это ориентированный ациклический граф операций - в нашем случае тензорных. Например, взгляните на представление в виде графа вычислений нашей первой модели (рисунок 1).
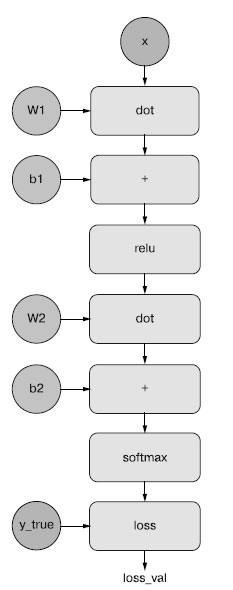
Рис.1. Представление в виде графа вычислений нашей первой двухслойной модели
Графы вычислений оказались чрезвычайно успешной абстракцией в информатике, поскольку позволяют рассматривать вычисления как данные: последовательность вычислений кодируется как машиночитаемая структура данных, которую можно передать другой программе. Например, представьте программу, которая получает один граф вычислений и возвращает другой, новый, реализующий крупномасштабную распределенную версию того же вычисления, - подобное решение позволило бы превращать любые вычисления в распределенные без необходимости писать логику распределения самостоятельно. А что насчет программы, которая получает граф вычислений и автоматически генерирует производную для выражения, которое представляет данный граф? Сделать это намного проще, если вычисления выражены в виде явной структуры данных, а не, скажем, строк символов ASCII в файле .py.
Для полноты картины рассмотрим несложный пример графа вычислений (рисунок 2) - упрощенную версию графа, изображенного на рисунке 1.
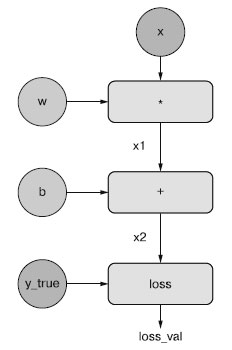
Рис.2. Пример простого графа вычислений
Здесь у нас имеется только один линейный слой, и все переменные являются скалярными. Мы берем две скалярные переменные w и b, скалярный вход х, и применяем к ним некоторые операции, чтобы получить на выходе у. В заключение мы используем функцию вычисления абсолютных потерь: loss_val = abs(y_true - у). Поскольку нам нужно обновить w и b так, чтобы минимизировать loss_val, мы должны вычислить grad(loss_val, b) и grad(loss_val, w).
Давайте выберем конкретные значения для "входных узлов" в графе, то есть входные значения х, y_true, w и b, и распространим их через все узлы графа сверху вниз, пока не достигнем loss_val. Это - прямой проход (рисунок 3).
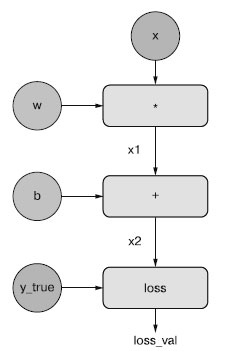
Рис.3. Прямой проход
Затем "обратим" граф: для каждого ребра в графе, идущего от A к B, создадим противоположное ребро от B к A и спросим, как сильно меняется B при изменении A. Иными словами, что такое grad(B, A)? Подпишем каждое обратное ребро этим значением. Данный обратный граф демонстрирует обратный проход (рисунок 4).
Рис.4. Обратный проход
Мы имеем следующие результаты:
- grad(loss_val, x2) = 1, потому что с изменением х2 на некоторую величину loss_val = abs(4 - х2) изменяется на ту же величину;
- grad(x2, х1) = 1, потому что с изменением х1 на некоторую величину х2 = х1 + b = х1 + 1 изменяется на ту же величину;
- grad(x2, b) = 1, потому что с изменением b на некоторую величину х2 = х1 + b = 6 + b изменяется на ту же величину;
- grad(x1, w) = 2, потому что с изменением w на некоторую величину х1 = х * w = 2 * w изменяется на величину, в два раза большую.
Применив цепное правило к обратному графу, можно получить производную узла по отношению к другому узлу, перемножив производные всех ребер на пути, соединяющем два узла. Например, grad(loss_val, w) = grad(loss_val, х2) * grad(x2, х1) * grad(x1, w) (рисунок 5).
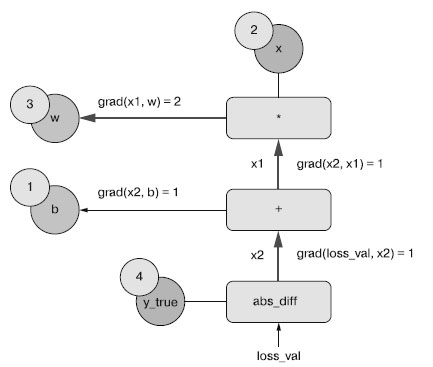
Рис.5. Путь от loss_val до w в обратном графе
Применение цепного правила к нашему графу дает нам искомое:
- grad(loss_val, w) = 1 * 1 * 2 = 2;
- grad(loss_val, b) = 1 * 1 = 1.
Если в обратном графе есть несколько путей, связывающих два узла, a и b, то получить grad(b, a) можно суммированием вкладов всех путей.
Вы только что увидели обратное распространение в действии! Обратное распространение - это просто применение цепного правила к графу вычислений и ничего более. Оно начинается с конечного значения потери и движется в обратном направлении, от верхних слоев к нижним, используя цепное правило для вычисления вклада каждого параметра в значение потери. Отсюда и название "обратное распространение": мы "распространяем в обратном направлении" вклады в потери различных узлов в графе .
В настоящее время нейронные сети конструируются с использованием современных фреймворков, поддерживающих автоматическое дифференцирование (таких как TensorFlow). Автоматическое дифференцирование основано на применении графов вычислений, подобных тем, что вы видели выше, и позволяет извлекать градиенты произвольных последовательностей дифференцируемых тензорных операций, не выполняя при этом никакой дополнительной работы, кроме записи прямого прохода. Когда создавались первые нейронные сети на C в 2000-х, приходилось писать реализацию градиентов вручную. Теперь благодаря современным инструментам автоматического дифференцирования нет необходимости самостоятельно реализовывать обратное распространение.
На следующем шаге мы рассмотрим объект GradientTape в TensorFlow.
