На этом шаге мы вернемся к первому примеру и прокомментируем его, используя изченный материал.
Мы подошли к концу изложения этого раздела, и теперь вы должны неплохо представлять, что происходит в недрах нейронной сети. То, что раньше казалось волшебным черным ящиком, сложилось в более ясную картину, изображенную на рисунке 1.
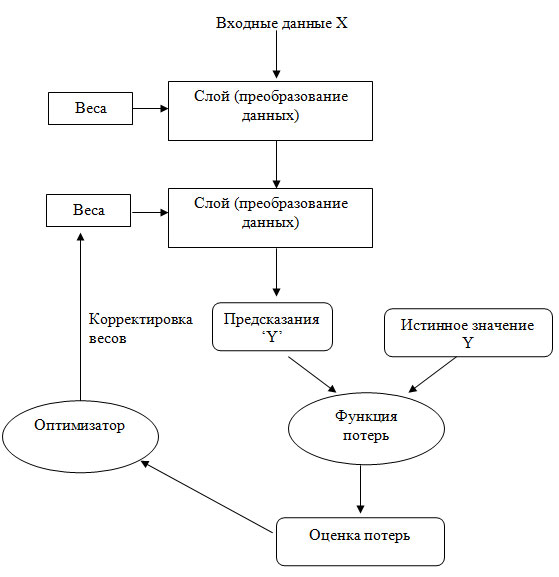
Рис.1. Связь между слоями, функцией потерь и оптимизатором в сети
Итак, у нас есть модель, состоящая из слоев, которая преобразует входные данные в прогнозы. Затем функция потерь сравнивает прогнозы с целевыми значениями, получая значение потерь: меру соответствия полученного моделью прогноза ожидаемому результату. Позже оптимизатор использует значение потерь для корректировки весов модели.
Давайте вернемся назад, к первому примеру, и рассмотрим каждую его часть через призму полученных знаний.
Вот наши входные данные:
(train_images, train_labels), (test_images, test_labels) = mnist.load_data() train_images = train_images.reshape((60000, 28 * 28)) train_images = train_images.astype("float32") / 255 test_images = test_images.reshape((10000, 28 * 28)) test_images = test_images.astype("float32") / 255
Теперь вам известно, что входные изображения хранятся в тензорах NumPy типа float32, имеющих форму (60000, 784) (обучающие данные) и (10000, 784) (контрольные данные) соответственно.
Вот наша сеть:
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
Вы уже знаете, что эта модель состоит из цепочки двух слоев Dense, каждый из которых применяет к входным данным несколько простых тензорных операций, а также что эти операции вовлекают весовые тензоры. Весовые тензоры, являющиеся атрибутами слоев, - это место, где запоминаются знания, накопленные моделью.
Вот как выглядел этап компиляции:
model.compile(optimizer="rmsprop", loss="sparse_categorical_crossentropy", metrics=["accuracy"])
Сейчас вы понимаете, что sparse_categorical_crossentropy - это функция потерь, которая используется в качестве сигнала обратной связи для обучения весовых тензоров и которую этап обучения стремится свести к минимуму. Вы также знаете, что снижение потерь достигается за счет применения алгоритма стохастического градиентного спуска на небольших пакетах. Точные правила, управляющие конкретным применением градиентного спуска, определяются оптимизатором rmsprop, который передается в первом аргументе.
Наконец, вот как выглядел цикл обучения:
model.fit(train_images, train_labels, epochs=5, batch_size=128)
Теперь вам понятно, что происходит в вызове fit: модель начинает перебирать обучающие данные мини-пакетами по 128 образцов и выполняет пять итераций (каждая итерация по всем обучающим данным называется эпохой). Для каждого мини-пакета модель вычисляет градиенты потерь относительно весов (с использованием алгоритма обратного распространения ошибки, который использует цепное правило дифференциального и интегрального исчисления) и изменяет значения весов в соответствующем направлении.
В течение пяти эпох сеть выполнит 2345 изменений градиента (по 469 на эпоху), после чего потери модели окажутся достаточно низкими, чтобы она могла классифицировать рукописные цифры с высокой точностью.
Итак, вы знаете большую часть того, что нужно знать о нейронных сетях. Давайте подтвердим это, повторно реализовав в TensorFlow упрощенную версию нашего первого примера.
На следующем шаге мы рассмотрим повторную реализацию первого примера в TensorFlow.
