На этом шаге мы рассмотрим особенности организации такой проверки.
Для контроля точности модели создадим проверочный набор, выбрав 1000 образцов из набора обучающих данных.
Пример 4.17. Создание проверочного набора
x_val = x_train[:1000] partial_x_train = x_train[1000:] y_val = y_train[:1000] partial_y_train = y_train[1000:]
Теперь проведем обучение модели в течение 20 эпох.
Пример 4.18. Обучение модели
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
И наконец, выведем графики кривых потерь и точности (рисунки 1 и 2).
Пример 4.19. Формирование графиков потерь на этапах обучения и проверки
import matplotlib.pyplot as plt loss = history.history["loss"] val_loss = history.history["val_loss"] epochs = range(1, len(loss) + 1) plt.plot(epochs, loss, "bo", label="Потери на этапе обучения") plt.plot(epochs, val_loss, "b", label="Потери на этапе проверки") plt.title("Потери на этапах обучения и проверки") plt.xlabel("Эпохи") plt.ylabel("Потери") plt.legend() plt.show()
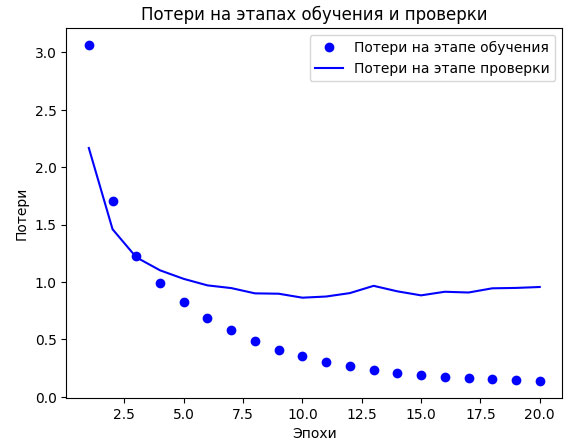
Рис.1. Потери на этапах обучения и проверки
Пример 4.20. Формирование графиков точности на этапах обучения и проверки
plt.clf() acc = history.history["accuracy"] val_acc = history.history["val_accuracy"] plt.plot(epochs, acc, "bo", label="Точность на этапе обучения") plt.plot(epochs, val_acc, "b", label="Точность на этапе проверки") plt.title("Точность на этапах обучения и проверки") plt.xlabel("Эпохи") plt.ylabel("Точность") plt.legend() plt.show()
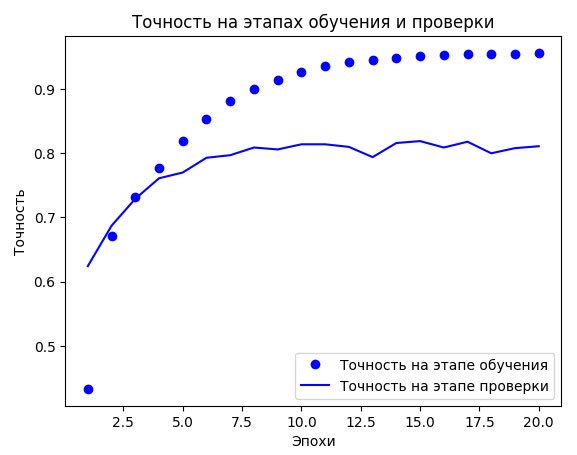
Рис.2. Точность на этапах обучения и проверки
Переобучение сети наступает после девятой эпохи. Давайте теперь обучим новую модель в течение девяти эпох и затем оценим получившийся результат на контрольных данных.
Пример 4.21. Обучение новой модели с нуля
model = keras.Sequential([
layers.Dense(64, activation="relu"),
layers.Dense(64, activation="relu"),
layers.Dense(46, activation="softmax")
])
model.compile(optimizer="rmsprop",
loss="categorical_crossentropy",
metrics=["accuracy"])
model.fit(x_train,
y_train,
epochs=9,
batch_size=512)
results = model.evaluate(x_test, y_test)
Конечные результаты:
print(results)
[0.9177919030189514, 0.796972393989563]
Данное решение достигло точности ~80% . В сбалансированной задаче бинарной классификации точность чисто случайного классификатора составила бы 50% . Но мы имеем 46 классов, и они могут быть представлены неодинаково. Интересно, какую точность дал бы простой случайный классификатор в этом случае? Проверим эмпирически, реализовав такой классификатор на скорую руку:
import copy test_labels_copy = copy.copy(test_labels) np.random.shuffle(test_labels_copy) hits_array = np.array(test_labels) == np.array(test_labels_copy) print(hits_array.mean()) 0.18744434550311664
Как видите, случайный классификатор показал точность классификации около 19% - и в этом свете результаты нашей модели выглядят очень неплохо.
На следующем шаге мы рассмотрим предсказания на новых данных.
