На этом шаге мы рассмотрим случай, когда требуется более одного классификатора.
Как вы имели возможность убедиться, рассмотренные нами простые предикторы и классификаторы, относящиеся к числу тех, которые получают некоторые входные данные, выполняют соответствующие вычисления и выдают ответ, довольно эффективны. И все же их возможностей недостаточно для решения более интересных задач, к которым мы намереваемся применять методы нейронных сетей.
Ограничения линейного классификатора продемонстрированы ниже на простом, но весьма показательном примере. Но почему мы должны заниматься этим вместо того, чтобы сразу же перейти к обсуждению нейронных сетей? Дело в том, что от понимания сути указанных ограничений зависит один из ключевых элементов проектирования нейронных сетей, так что этот вопрос стоит того, чтобы его обсудить.
Мы отойдем от темы садовых жучков и обратимся к логическим (булевым) функциям. Не беспокойтесь, если эта терминология вам ни о чем не говорит. Джордж Буль - математик и философ, с именем которого связаны такие простые функции, как логические И и ИЛИ.
Функции булевой логики - это своего рода "мыслительные" функции со своим языком. Если мы говорим "Ты получишь пудинг только в том случае, если уже съел овощи И все равно голоден", то мы используем булеву функцию И. Результат булевой функции И истинен только тогда, когда истинны (выполняются) оба условия. Он не будет истинным, если истинно только одно из условий. Поэтому, если я голоден, но еще не съел овощи, то не получу свой пудинг.
Аналогично, если мы говорим "Ты можешь погулять в парке, если сегодня выходной ИЛИ у тебя отпуск", то используем булеву функцию ИЛИ. Результат булевой функции ИЛИ истинен, если истинным является хотя бы одно из условий. Вовсе не обязательно, чтобы все условия были истинными, как в случае функции И. Поэтому, если сегодня не выходной день, но у меня отпуск, то я могу погулять в парке.
Ранее мы представляли функцию в виде машины, которая принимает некоторые входные данные, выполняет определенные действия и выдает один ответ.
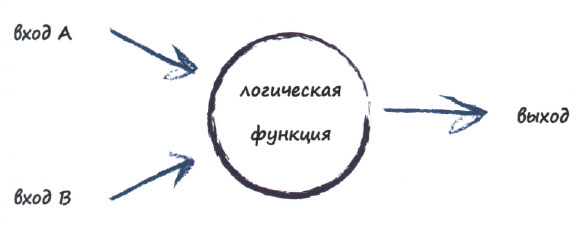
Значение истина часто представляется в компьютерах как число 1, а значение ложь - как число 0. В приведенной ниже таблице результаты работы логических функций И и ИЛИ представлены с использованием этой лаконичной нотации для всех комбинаций входных значений А и В.
| Входное значение А | Входное значение B | Логическое И | Логическое ИЛИ |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Здесь отчетливо видно, что результат функции И будет истинным только тогда, когда истинны и А, и В.
Булевы функции играют очень важную роль в информатике, и первые электронные вычислительные устройства фактически собирались из крохотных электрических схем, выполняющих логические операции. Даже арифметические операции выполнялись с использованием этих схем, которые сами по себе всего лишь выполняли простые булевы операции.
Представьте себе простой линейный классификатор, который должен использовать тренировочный набор данных для выяснения того, управляются ли данные логической функцией. Задачи такого рода естественным образом возникают перед учеными, исследующими причинно-следственные связи или корреляцию наблюдаемых величин. Например, требуется найти ответ на следующий вопрос: "Повышается ли вероятность заболевания малярией в тех местностях, в которых постоянно идут дожди И температура превышает 35 градусов?" Или такой: "Повышается ли вероятность заболевания малярией, если выполняется любое (булева функция ИЛИ) из этих условий?"
Взгляните на приведенную ниже диаграмму, где значения на двух входах логической функции, А и В, представляют координаты точек на графике. Вы видите, что только в том случае, когда оба входных значения истинны, т.е. каждое из них равно 1, выходной результат, выделенный зеленым цветом, является истинным. Ложные выходные значения обозначены красным цветом.
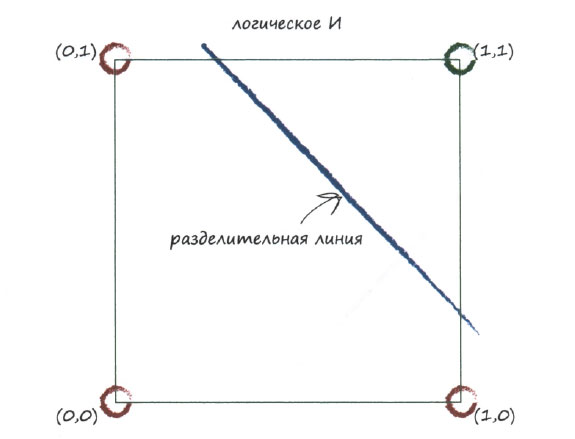
На диаграмме также показана прямая линия, отделяющая красную область от зеленой. Эта линия представляет линейную функцию, которую можно использовать для обучения линейного классификатора, что мы делали ранее.
Мы не будем проводить соответствующие вычисления, как в предыдущих примерах, поскольку ничего принципиально нового это не даст.
В действительности можно было бы предложить много других вариантов проведения разделительной линии, которые работали бы столь же удовлетворительно, но главный вывод из этого примера заключается в том, что простой линейный классификатор вида у=ах+b можно обучить работе с булевой функцией И.
А теперь взгляните на аналогичное графическое представление булевой функции ИЛИ.
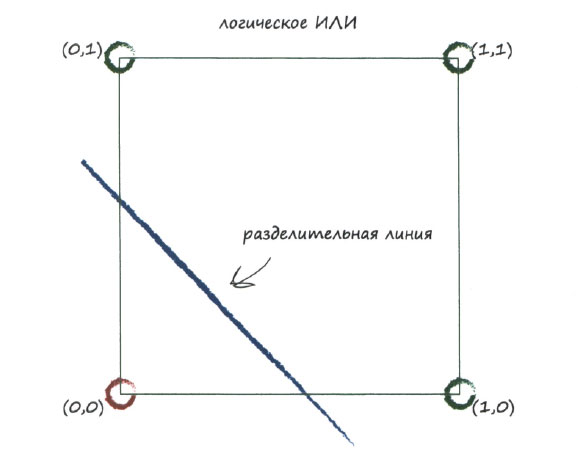
На этот раз красной оказалась лишь точка (0,0), поскольку ей соответствуют ложные значения на обоих входах, А и В. Во всех других комбинациях значений хотя бы одно из них является истинным, и поэтому для них результат является истинным. Вся прелесть этой диаграммы заключается в том, что она наглядно демонстрирует возможность обучения линейного классификатора работе с функцией ИЛИ.
На следующем шаге мы закончим изучение этого вопроса.
