На этом шаге мы введем понятие "функция активации".
Рассмотрим, как работает нейрон. Он принимает поступающий электрический сигнал и вырабатывает другой электрический сигнал. Это очень напоминает работу моделей классификатора или предиктора, которые получают некоторые входные данные, выполняют определенные вычисления и выдают результат.
Так можем ли мы представить нейроны в виде линейных функций по аналогии с тем, что мы делали до этого? Нет, хотя сама по себе эта идея неплохая. Вырабатываемый нейроном выходной сигнал не является простой линейной функцией входного сигнала, т.е. выходной сигнал нельзя представить в виде
выход = (константа * вход) + (другая константа).
Согласно результатам наблюдений нейроны не реагируют немедленно, а подавляют входной сигнал до тех пор, пока он не возрастет до такой величины, которая запустит генерацию выходного сигнала. Это можно представить себе как наличие некоего порогового значения, которое должно быть превышено, прежде чем будет сгенерирован выходной сигнал. Сравните поведение воды в чашке: вода не сможет выплеснуться, пока чашка не наполнится. Интуитивно это понятно - нейроны пропускают лишь сильные сигналы, несущие полезную информацию, но не слабый шум. Идея вырабатывания выходного сигнала лишь в случаях, когда амплитуда входного сигнала достигает достаточной величины, превышающей некоторый порог, проиллюстрирована ниже в графическом виде.

Функция, которая получает входной сигнал, но генерирует выходной сигнал с учетом порогового значения, называется функцией активации. С математической точки зрения существует множество таких функций, которые могли бы обеспечить подобный эффект. В качестве примера можно привести ступенчатую функцию.
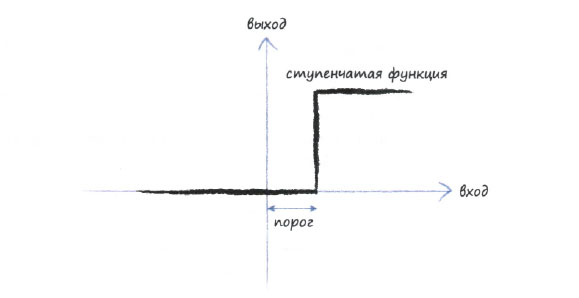
Нетрудно заметить, что для слабых входных значений выходное значение равно нулю. Но стоит превысить входной порог, как на выходе появляется сигнал. Искусственный нейрон с таким поведением напоминал бы настоящий биологический нейрон. Это очень хорошо описывается термином, который используется учеными: они говорят, что нейрон возбуждается при достижении входным сигналом порогового значения.
Ступенчатую функцию можно усовершенствовать. Представленную ниже S-образную функцию называют сигмоидой, или сигмоидальной функцией. Резкие прямоугольные границы ступенчатой функции в ней сглажены, что делает ее более естественной и реалистичной. Природа не любит острых углов!
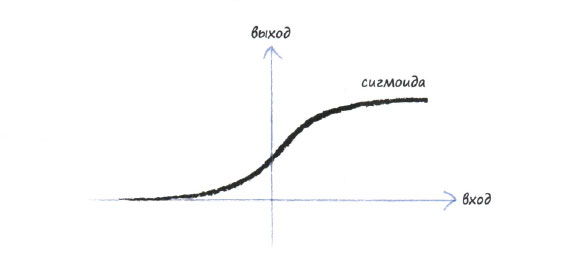
Сглаженная S-образная сигмоида - это и есть то, что мы будем использовать для создания собственной нейронной сети. Исследователями в области искусственного интеллекта используются также другие функции аналогичного вида, но сигмоида проста и очень популярна, так что она будет для нас отличным выбором.
Сигмоида, которую иногда называют также логистической функцией, описывается следующей формулой:

Это выражение не настолько устрашающее, как поначалу может показаться. Буквой е в математике принято обозначать константу, равную 2,71828... Это очень интересное число, которое встречается во многих областях математики и физики, а причина, по которой в нем использовано многоточие (...), заключается в том, что запись десятичных знаков может быть продолжена до бесконечности. Для подобных чисел существует причудливое название - трансцендентные числа. Все это, конечно, интересно, но для наших целей вполне достаточно считать, что это число просто равно 2,71828. Входное значение берется с отрицательным знаком, и е возводится в степень -х. Результат прибавляется к 1, что дает нам 1+е-х. Наконец, мы обращаем последнюю сумму, т.е. делим 1 на 1+е-х Это и есть то, что делает приведенная выше функция с входным значением х для того, чтобы предоставить нам выходное значение у. Поэтому на самом деле ничего страшного в ней нет.
Просто ради интереса следует отметить, что при нулевом значении х выражение ех принимает значение 1, поскольку возведение любого числа в нулевую степень всегда дает 1. Поэтому у становится равным 1 / (1 + 1) или просто 1/2, т.е. половине. Следовательно, базовая сигмоида пересекает ось у при у=1/2.
Существует еще одна, очень веская, причина для того, чтобы из множества всех S-образных функций, которые можно было бы использовать для определения выходного значения нейрона, выбрать именно сигмоиду. Дело в том, что выполнять расчеты с сигмоидой намного проще, чем с любой другой S-образной функцией, и вскоре вы на практике убедитесь в том, что это действительно так. еще остаются загадкой, но мы знаем о нейронах достаточно много для того, чтобы можно было предложить различные способы выполнения вычислений, т.е. различные способы решения задач.
На следующем шаге мы закончим изучение этого вопроса.
