На этом шаге мы продолжим работу с примером, в частности займемся скрытым слоем.

    Продолжим нашу работу и определим комбинированный сглаженный сигнал для скрытого слоя. Кроме того, мы должны присвоить ему описательное имя, снабженное индексом, который указывает на то, что это входной сигнал для скрытого, а не последнего слоя. Назовем соответствующую матрицу Х_{скрытый}:

    Мы не собираемся выполнять вручную все действия, связанные с перемножением матриц. Выполнение этой трудоемкой работы мы будем поручать компьютеру, ведь именно с этой целью мы используем матрицы. В данном случае готовый ответ выглядит так.

    Этот ответ был получен с помощью компьютера, и вы научитесь делать это, используя язык программирования Python, о чем мы поговорим далее. Мы не будем заниматься этим сейчас, чтобы пока что не отвлекаться на обсуждение программного обеспечения.

    Итак, мы располагаем комбинированными сглаженными входными сигналами скрытого промежуточного слоя, значения которых равны 1,16; 0,42 и 0,62. Для выполнения всех необходимых вычислений были использованы матрицы. Это достижение, которым мы вправе гордиться!

    Отобразим входные сигналы для скрытого второго слоя на диаграмме.

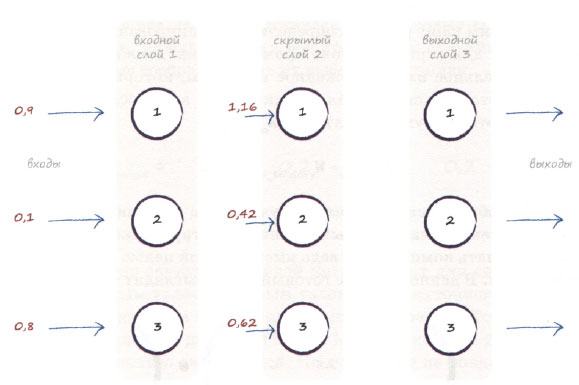
    Пока что все хорошо, но нам еще остается кое-что сделать. Как вы помните, чтобы отклик слоя на входной сигнал как можно лучше имитировал аналогичный реальный процесс, мы должны применить к узлам функцию активации. Так и поступим:

    Oскрытый = сигмоида(Хскрытый)

    Применяя сигмоиду к каждому элементу матрицы Х_{скрытый}, мы получаем матрицу выходных сигналов скрытого промежуточного слоя.

    Для уверенности давайте проверим, правильно ли вычислен первый элемент. Наша сигмоида имеет вид

              1
      y = ---------      
           1 + e-x

    Нетрудно заметить, что все возможные значения этой функции находятся в пределах от 0 до 1. Вернитесь немного назад и взгляните на график логистической функции, если хотите убедиться в том, что это действительно так.

    Ух! Давайте немного передохнем и подытожим, что мы к этому времени успели сделать. Мы рассчитали прохождение сигнала через промежуточный слой, т.е. определили значения сигналов на его выходе. Для полной ясности уточним, что эти значения были получены путем применения функции активации к комбинированным входным сигналам промежуточного слоя. Обновим диаграмму в соответствии с этой новой информацией

    Если бы это была двухслойная нейронная сеть, то мы сейчас остановились бы, поскольку получили выходные сигналы второго слоя. Однако мы продолжим, поскольку есть еще и третий слой.

    На следующем шаге мы закончим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг