На этом шаге мы рассмотрим особенности задания случайных значений.
Здесь применима та же аргументация, что и в случае входных и выходных сигналов. Мы должны избегать больших начальных значений весовых коэффициентов, поскольку использование функции активации в этой области значений может приводить к насыщению сети, о котором мы только что говорили, и снижению способности сети обучаться на лучших значениях.
Один из возможных вариантов - прибегнуть к выбору значений из случайного равномерного распределения чисел в диапазоне от -1,0 до +1,0. Это гораздо лучше, чем использовать, скажем, диапазон чисел от -1000 до +1000.
Возможен ли лучший вариант? Вполне вероятно.
Математики и ученые-компьютерщики разработали подходы, позволяющие определять эмпирические правила для задания случайных начальных значений весовых коэффициентов в зависимости от конкретной конфигурации сети и используемой функции активации. Соответствующие рецепты в высшей степени специфичны, но, невзирая на это, мы рискнем подступиться к ним!
Мы не будем вдаваться в детали математических выкладок, но центральная идея заключается в том, что если на узел нейронной сети поступает множество сигналов, причем поведение этих сигналов хорошо определено, они не достигают слишком больших значений и не распределены каким-то невероятным образом, то весовые коэффициенты не должны нарушать такое состояние сигналов в процессе их объединения и обработки функцией активации. Иными словами, мы не должны использовать весовые коэффициенты, разрушающие результаты наших попыток тщательно масштабировать входные сигналы. Суть эмпирического правила, к которому пришли математики, заключается в том, что весовые коэффициенты инициализируются числами, случайно выбираемыми из диапазона, грубая оценка которого определяется обратной величиной квадратного корня из количества связей, ведущих к узлу. Таким образом, если к каждому узлу ведут три связи, то начальные значения весов не должны превышать значение 1 / (√3) = 0,577. Если же каждый узел имеет 100 входящих связей, то веса должны находиться в диапазоне, ограниченном значением l / (√l00) = 0,1.
Интуитивно это понятно. Некоторые слишком большие веса сместили бы функцию активации в область больших значений, что привело бы к ее насыщению. И чем больше связей приходится на узел, тем больше складывается весовых коэффициентов. Поэтому эмпирическое правило, которое уменьшает диапазон значений весовых коэффициентов с увеличением количества связей на узел, находит логическое объяснение.
Если вы уже знакомы с идеей выборочных значений, извлекаемых из распределений вероятностей, то поймете, что это правило фактически относится к нормальному распределению, для которого среднее значение равно нулю, а стандартное отклонение равно обратной величине корня из количества связей, ведущих к узлу. Однако не будем слишком строго придерживаться этой рекомендации, поскольку она предполагает выполнение довольно большого количества условий, которые не всегда соблюдаются, таких как альтернативное использование гиперболического тангенса th() в качестве функции активации и специфическое распределение входных сигналов.
Следующий график иллюстрирует в наглядной форме как простой подход, так и более сложный, в котором используется нормальное распределение.
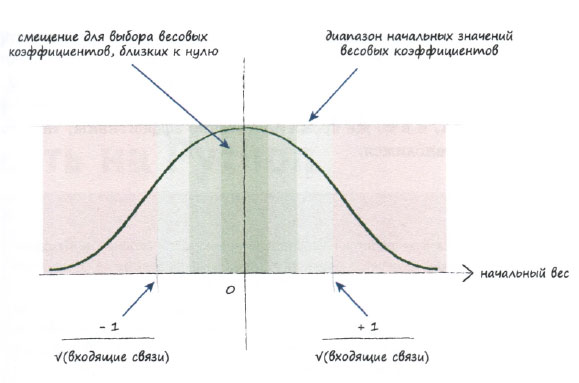
В любом случае никогда не задавайте для начальных весов равные значения, особенно нулевые. Это был бы крайне неудачный вариант!
Этот вариант был бы неудачным по той причине, что в таком случае все узлы сети получили бы одинаковые сигналы, и сигналы на выходе каждого узла были бы одинаковыми. Если затем приступить к обновлению весов с использованием механизма обратного распространения ошибки, то ошибка распределится равномерно. Вы ведь не забыли, что ошибка распределяется между узлами пропорционально весам. Это приведет к одинаковым поправкам для всех весовых коэффициентов, что, в свою очередь, вновь приведет к весам, имеющим одинаковые значения. Подобная симметрия играет крайне отрицательную роль, ведь если правильно натренированная сеть должна иметь неодинаковые значения весовых коэффициентов (что характерно для большинства задач), то вы никогда не достигнете этого состояния.
Еще худший выбор - нулевые значения, поскольку они полностью "убивают" входной сигнал. В этом случае функция обновления весов, которая зависит от входных сигналов, обнуляется, тем самым полностью исключая саму возможность обновления весов.
Существует множество других мер, которые можно предпринять для улучшения процедур подготовки входных данных, задания весовых коэффициентов и организации желаемых выходных значений. Учитывая цель изложения данные идеи достаточно просты, чтобы быть понятными, и в то же время достаточно эффективны, так что на этом мы и остановимся.
Резюме
- Нейронные сети не работают удовлетворительно, если входные и выходные данные, а также начальные значения весовых коэффициентов не согласуются со структурой сети и спецификой конкретной задачи.
- Распространенной проблемой является насыщение сети - ситуация, когда большие значения сигналов, часто обусловленные большими значениями весовых коэффициентов, приводят к сигналам, попадающим в область близких к нулю значений градиента функции активации. Результатом этого является снижение способности сети обучаться на лучших значениях весовых коэффициентов.
- Другую проблему представляют нулевые значения сигналов или весов. Эти значения также полностью лишают сеть возможности обучаться на лучших значениях весовых коэффициентов.
- Значения весовых коэффициентов внутренних связей должны быть случайными и небольшими, но не нулевыми. Иногда используют более сложные правила, включающие, например, уменьшение значений весовых коэффициентов с увеличением количества связей, ведущих к узлу.
- Входные сигналы должны масштабироваться до небольших, но ненулевых значений. Обычно используют диапазоны значений от 0,01 до 0,99 и от -1.0 до +1,0 в зависимости от того, какой из них лучше соответствует специфике задачи.
- Выходные сигналы должны находиться в пределах диапазона, который способна обеспечить функция активации. Значения, меньшие или равные 0 и большие или равные 1, не совместимы с логистической сигмоидой. Установка тренировочных целевых значений за пределами допустимого диапазона приведет к еще большим значениям весов и в конечном счете к насыщению сети. Неплохим диапазоном является диапазон значений от 0,01 до 0,99.
Со следующего шага мы начнем создавать свою нейронную сеть.
