На этом шаге мы рассмотрим особенности подготовки таких даных.
Теперь, когда вы уже знаете, как получить данные из файлов MNIST и извлечь из них нужные записи, мы можем воспользоваться этим для визуализации данных. Мы хотим использовать эти данные для обучения нашей нейронной сети, но сначала мы должны продумать, как их следует подготовить, прежде чем предоставлять сети.
Вы уже видели, что нейронные сети работают лучше, если как входные, так и выходные данные конфигурируются таким образом, чтобы они оставались в диапазоне значений, оптимальном для функций активации узлов нейронной сети.
Первое, что мы должны сделать, - это перевести значения цветовых кодов из большего диапазона значений 0-255 в намного меньший, охватывающий значения от 0,01 до 1,0. Мы намеренно выбрали значение 0,01 в качестве нижней границы диапазона, чтобы избежать упомянутых ранее проблем с нулевыми входными значениями, поскольку они могут искусственно блокировать обновление весов. Нам необязательно выбирать значение 0,99 в качестве верхней границы допустимого диапазона, поскольку нет нужды избегать значений 1,0 для входных сигналов. Лишь выходные сигналы не могут превышать значение 1,0.
Деление исходных входных значений, изменяющихся в диапазоне 0-255, на 255 приведет их к диапазону 0-1,0. Последующее умножение этих значений на коэффициент 0,99 приведет их к диапазону 0,0-0,99. Далее мы инкрементируем их на 0,01, чтобы вместить их в желаемый диапазон 0,01-1,0. Все эти действия реализует следующий код на языке Python.
scaled_input = (numpy.asfarray(all_values[1:]) / 255 * 0.99) + 0.01 print(scaled_input)
Результирующий вывод данных подтверждает, что они действительно принадлежат к диапазону значений от 0,01 до 1,00.
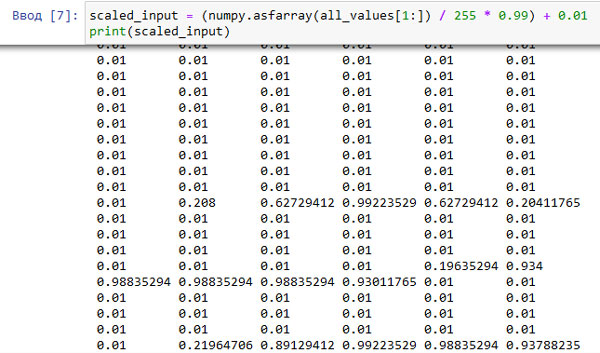
Рис.1. Результат нормализации
Итак, мы осуществили подготовку данных MNIST путем их масштабирования и сдвига и теперь можем подавать их на вход нашей нейронной сети как с целью ее тренировки, так и с целью опроса.
На этом этапе нам также нужно продумать, что делать с выходными значениями нейронной сети. Ранее вы видели, что выходные значения должны укладываться в диапазон значений, обеспечиваемый функцией активации. Используемая нами логистическая функция не может выдавать такие значения, как -2,0 или 255. Ее значения охватывают диапазон чисел от 0,0 до 1,0, а фактически вы никогда не получите значений 0,0 или 1,0, поскольку логистическая функция не может их достигать и лишь асимптотически приближается к ним. Таким образом, по-видимому, нам придется масштабировать выходные значения в процессе тренировки сети.
Но вообще-то, мы должны задать самим себе вопрос более глубокого содержания. Что именно мы должны получить на выходе нейронной сети? Должно ли это быть изображение ответа? В таком случае нам нужно иметь 28 * 28 = 784 выходных узла.
Если мы вернемся на шаг назад и задумаемся над тем, чего именно мы хотим от нейронной сети, то поймем, что мы просим ее классифицировать изображение и присвоить ему корректный маркер. Таким маркером может быть одно из десяти чисел в диапазоне от 0 до 9. Это означает, что выходной слой сети должен иметь 10 узлов, по одному на каждый возможный ответ, или маркер. Если ответом является "0", то активизироваться должен первый узел, тогда как остальные узлы должны оставаться пассивными. Если ответом является "9", то активизироваться должен последний узел выходного слоя при пассивных остальных узлах. Следующая иллюстрация поясняет эту схему на нескольких примерах выходных значений.
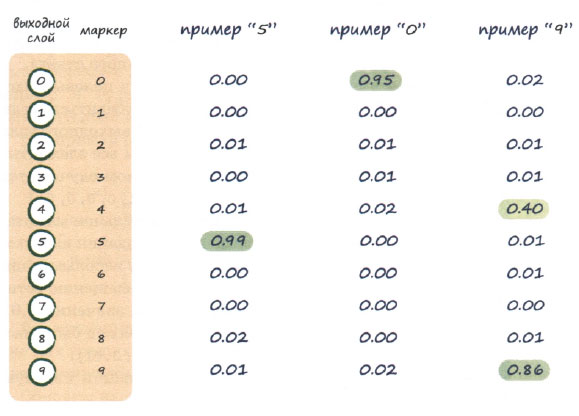
Первый пример соответствует случаю, когда сеть распознала входные данные как цифру "5". Вы видите, что наибольший из исходящих сигналов выходного слоя принадлежит узлу с меткой "5". Не забывайте о том, что это шестой по счету узел, потому что нумерация узлов начинается с нуля. Все довольно просто. Остальные узлы производят сигналы небольшой величины, близкие к нулю. Вывод нулей мог оказаться следствием ошибок округления, но в действительности, как вы помните, функция активации никогда не допустит фактическое нулевое значение.
Следующий пример соответствует рукописному "0". Наибольшую величину здесь имеет сигнал первого выходного узла, ассоциируемый с меткой "0".
Последний пример более интересен. Здесь самый большой сигнал генерирует последний узел, соответствующий метке "9". Однако и узел с меткой "4" дает сигнал средней величины. Обычно нейронная сеть должна принимать решение, основываясь на наибольшем сигнале, но, как видите, в данном случае она отчасти считает, что правильным ответом могло бы быть и "4". Возможно, рукописное начертание символа затруднило его надежное распознавание? Такого рода неопределенности встречаются в нейронных сетях, и вместо того, чтобы считать их неудачей, мы должны рассматривать их как полезную подсказку о существовании другого возможного ответа.
Отлично! Теперь нам нужно превратить эти идеи в целевые массивы для тренировки нейронной сети. Как вы могли убедиться, если тренировочный пример помечен маркером "5", то для выходного узла следует создать такой целевой массив, в котором малы все элементы, кроме одного, соответствующего маркеру "5". В данном случае этот массив мог бы выглядеть примерно так: [0,0,0,0,0,1,0,0,0,0].
В действительности эти числа нуждаются в дополнительном масштабировании, поскольку мы уже видели, что попытки создания на выходе нейронной сети значений 0 и 1, недостижимых в силу использования функции активации, приводят к большим весам и насыщению сети. Следовательно, вместо этого мы будем использовать значения 0,01 и 0,99, и потому целевым массивом для маркера "5" должен быть массив [0.01, 0.01, 0.01, 0.01, 0.01, 0.99, 0.01, 0.01, 0.01, 0.01].
А вот как выглядит код на языке Python, создающий целевую матрицу.
# количество выходных узлов - 10 (пример) onodes = 10 targets = numpy.zeros(onodes) + 0.01 targets[int(all_values[0])] = 0.99
Первая строка после комментария просто устанавливает количество выходных узлов равным 10, что соответствует нашему примеру с десятью маркерами.
Во второй строке с помощью удобной функции numpy.zeros() создается массив, заполненный нулями. Желаемые размер и конфигурация массива задаются параметром при вызове функции. В данном случае создается одномерный массив, размер onodes которого равен количеству узлов в конечном выходном слое. Проблема нулей, которую мы только что обсуждали, устраняется путем добавления 0,01 к каждому элементу массива.
Следующая строка выбирает первый элемент записи из набора данных MNIST, являющийся целевым маркером тренировочного набора, и преобразует его в целое число. Вспомните о том, что запись читается из исходного файла в виде текстовой строки, а не числа. Как только преобразование выполнено, полученный целевой маркер используется для того, чтобы установить значение соответствующего элемента массива равным 0,99. Здесь все будет нормально работать, поскольку маркер "0" будет преобразован в целое число 0, являющееся корректным индексом данного маркера в массиве targets[]. Точно так же маркер "9" будет преобразован в целое число 9, и элемент targets[9] действительно является последним элементом этого массива.
Вот пример работы этого кода.
print(targets)
[ 0.99 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01]
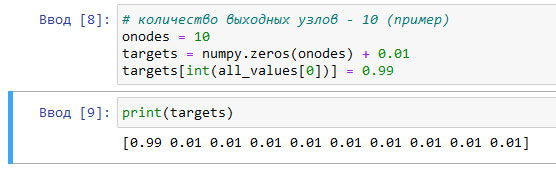
Рис.2. Результат работы приложения
Великолепно! Теперь мы знаем, как подготовить входные значения для тренировки и опроса нейронной сети, а выходные значения - для тренировки.
На следующем шаге мы закончим изучение этого вопроса.
