На этом шаге мы проанализируем зависимость получаемых результатов от значения коэффициента обучения.
Получение 95%-го показателя эффективности при тестировании набора данных MNIST нашей нейронной сетью, созданной на основе простейших идей и с использованием простого кода на языке Python, - это совсем неплохо, и ваше желание остановиться на этом можно было бы считать вполне оправданным.
Однако мы попытаемся улучшить разработанный к этому моменту код, внеся в него некоторые усовершенствования.
Прежде всего, мы можем попытаться настроить коэффициент обучения. Перед этим мы задали его равным 0,3, даже не тестируя другие значения.
Давайте удвоим это значение до величины 0,6 и посмотрим, как это скажется на способности нейронной сети обучаться. Выполнение кода с таким значением коэффициента обучения дает показатель эффективности 0,9047. Этот результат хуже прежнего. По-видимому, увеличение коэффициента обучения нарушает монотонность процесса минимизации ошибок методом градиентного спуска и сопровождается перескоками через минимум.
Повторим вычисления, установив коэффициент обучения равным 0,1. На этот раз показатель эффективности улучшился до 0,9523, что почти совпадает с результатом ранее упомянутого эталонного теста, который проводился с использованием тысячи скрытых узлов. Но ведь наш результат был получен с использованием намного меньшего количества узлов!
Что произойдет, если мы пойдем еще дальше и уменьшим коэффициент обучения до 0,01? Оказывается, это также приводит к уменьшению показателя эффективности сети до 0,9241. По-видимому, слишком малые значения коэффициента обучения снижают эффективность. Это представляется логичным, поскольку малые шаги уменьшают скорость градиентного спуска.
Описанные результаты представлены ниже в виде графика. Это не совсем научный подход, поскольку нам следовало бы провести такие эксперименты множество раз, чтобы исключить фактор случайности и влияние неудачного выбора маршрутов градиентного спуска, но в целом он позволяет проиллюстрировать общую идею о существовании некоего оптимального значения коэффициента обучения.
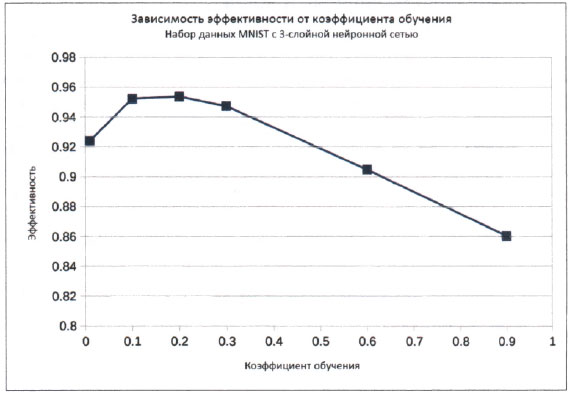
Рис.1. Зависимость эффективности от коэффициента обучения
Вид графика подсказывает нам, что оптимальным может быть значение в интервале от 0,1 до 0,3, поэтому испытаем значение 0,2. Показатель эффективности получится равным 0,9537. Мы видим, что этот результат немного лучше тех, которые мы имели при значениях коэффициента обучения, равных 0,1 или 0,3. Идею построения графиков вы должны взять на вооружение и в других сценариях, поскольку графики способствуют пониманию общих тенденций лучше, чем длинные числовые списки.
Итак, мы остановимся на значении коэффициента обучения 0,2, которое проявило себя как оптимальное для набора данных MNIST и нашей нейронной сети.
Кстати, если вы самостоятельно выполните этот код, то ваши оценки будут немного отличаться от приведенных здесь, поскольку процесс в целом содержит элементы случайности. Ваш случайный выбор начальных значений весовых коэффициентов не будет совпадать с нашим, а потому маршрут градиентного спуска для вашего кода будет другим.
На следующем шаге мы рассмотрим еще один способ улучшения результатов.
