На этом шаге мы рассмотрим еще один способ уличшения результатов.
Нашим следующим усовершенствованием будет многократное повторение циклов тренировки с одним и тем же набором данных. В отношении одного тренировочного цикла иногда используют термин эпоха. Поэтому сеанс тренировки из десяти эпох означает десятикратный прогон всего тренировочного набора данных. А зачем нам это делать? Особенно если для этого компьютеру потребуется 10, 20 или даже 30 минут? Причина заключается в том, что тем самым мы обеспечиваем большее число маршрутов градиентного спуска, оптимизирующих весовые коэффициенты.
Посмотрим, что нам дадут две тренировочные эпохи. Для этого мы должны немного изменить код, предусмотрев в нем дополнительный цикл выполнения кода тренировки. В приведенном ниже коде внешний цикл выделен жирным шрифтом, чтобы сделать его более заметным.
[In 4]: # тренировка нейронной сети # переменная epochs указывает, сколько раз тренировочный # набор данных используется для тренировки сети epochs = 2 for е in range(epochs): # перебрать все записи в тренировочном наборе данных for record in training_data_list: # получить список значений, используя символы запятой (',') # в качестве разделителей all_values = record.split(',') # масштабировать и сместить входные значения inputs = (numpy.asfarray(all_values[1:]) / 255 * 0.99) + 0.01 # создать целевые выходные значения (все равны 0,01, за исключением # желаемого маркерного значения, равного 0,99) targets = numpy.zeros(output_nodes) + 0.01 # all_values[0] - целевое маркерное значение для данной записи targets[int(all_values[0])] = 0.99 n.train(inputs, targets)
Результирующий показатель эффективности для двух эпох составляет 0,9579, что несколько лучше показателя для одной эпохи.
Подобно тому, как мы настраивали коэффициент обучения, проведем эксперимент с использованием различного количества эпох и построим график зависимости показателя эффективности от этого фактора. Интуиция подсказывает нам, что чем больше тренировок, тем выше эффективность. Но можно предположить, что слишком большое количество тренировок чревато ухудшением эффективности из-за так называемого переобучения сети на тренировочных данных, снижающего эффективность при работе с незнакомыми данными. Фактора переобучения следует опасаться в любых видах машинного обучения, а не только в нейронных сетях.
В данном случае мы имеем следующие результаты.
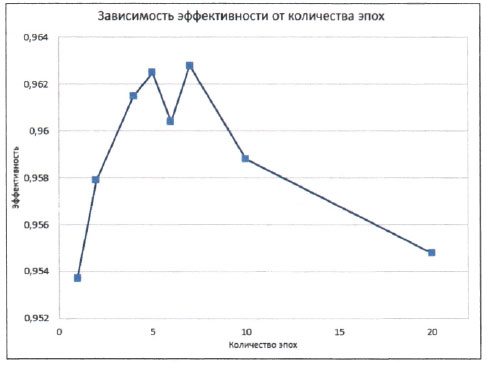
Теперь пиковое значение эффективности составляет 0,9628, или 96,28%, при семи эпохах.
Как видите, результаты оказались не столь предсказуемыми, как ожидалось. Оптимальное количество эпох - 5 или 7. При больших значениях эффективность падает, что может быть следствием переобучения. Провал при 6 эпохах, по всей вероятности, обусловлен неудачными параметрами цикла, которые привели градиентный спуск к ложному минимуму. На самом деле можно было ожидать большей вариации результатов, поскольку мы не проводили множества экспериментов для каждой точки данных, чтобы уменьшить вариацию, вызванную случайными факторами. Именно поэтому мы оставили эту странную точку, соответствующую шести эпохам, чтобы напомнить вам, что по самой своей сути обучение нейронной сети - это случайный процесс, который иногда может работать не очень хорошо, а иногда и очень плохо.
Другое возможное объяснение - это то, что коэффициент обучения оказался слишком большим для большего количества эпох. Повторим эксперимент, уменьшив коэффициент обучения с 0,2 до 0,1, и посмотрим, что произойдет.
На следующем графике новые значения эффективности при коэффициенте обучения 0,1 представлены вместе с предыдущими результатами, чтобы их было легче сравнить между собой.
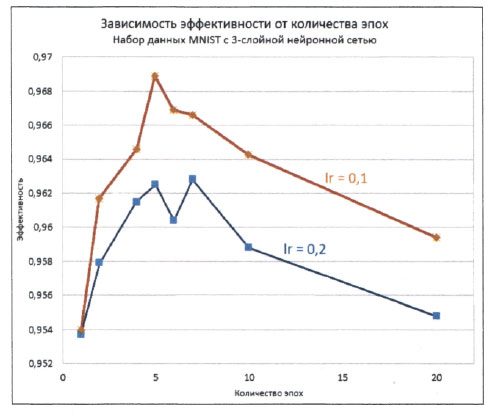
Как нетрудно заметить, уменьшение коэффициента обучения действительно привело к улучшению эффективности при большом количестве эпох. Пиковому значению 0,9689 соответствует вероятность ошибок, равная 3%, что сравнимо с эталонными результатами, указанными на сайте Яна Лекуна по адресу http://yann.lecun.com/exdb/mnist/.
Интуиция подсказывает нам, что если мы планируем использовать метод градиентного спуска при значительно большем количестве эпох, то уменьшение коэффициента обучения (более короткие шаги) в целом приведет к выбору лучших маршрутов минимизации ошибок. Вероятно, 5 эпох - это оптимальное количество для тестирования нашей нейронной сети с набором данных MNIST. Вновь обращу ваше внимание на то, что мы сделали это довольно ненаучным способом. Правильно было бы выполнить эксперимент по нескольку раз для каждого сочетания значений коэффициента обучения и количества эпох с целью минимизации влияния фактора случайности, присущего методу градиентного спуска.
На следующем шаге мы рассмотрим изменение конфигурации сети.
