На этом шаге мы проведем небольшие эксперименты, дополнив тренировачные данные.
Создадим новый блокнот Python с имеющимся кодом нейронной сети, но с дополнительными тренировочными примерами, созданными путем поворота исходных изображений на 10 градусов в обе стороны.
[In 1]: # Код для создания 3-слойной нейронной сети вместе с # кодом для ее обучения с помощью набора данных MNIST. # (с) Tariq Rashid, 2016 # лицензия GPLv2 import numpy # библиотека scipy.special содержит сигмоиду expit() import scipy.special # библиотека для графического отображения массивов import matplotlib.pyplot # гарантировать размещение графики в данном блокноте, # а не в отдельном окне %matplotlib inline # scipy.ndimage для поворота изображения import scipy.ndimage # определение класса нейронной сети class neuralNetwork: # инициализировать нейронную сеть def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate): # задать количество узлов во входном, скрытом и выходном слое self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes # Матрицы весовых коэффициентов связей wih (между входным и скрытым # слоями) и who (между скрытым и выходным слоями). # Весовые коэффициенты связей между узлом i и узлом j следующего слоя # обозначены как w_i_j: # w11 w21 # w12 w22 и т.д. self.wih = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes)) self.who = numpy.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes)) # коэффициент обучения self.lr = learningrate # использование сигмоиды в качестве функции активации self.activation_function = lambda x: scipy.special.expit(x) # тренировка нейронной сети def train(self, inputs_list, targets_list): # преобразовать список входных значений в двухмерный массив inputs = numpy.array(inputs_list, ndmin=2).T targets = numpy.array(targets_list, ndmin=2).T # рассчитать входящие сигналы для скрытого слоя hidden_inputs = numpy.dot(self.wih, inputs) # рассчитать исходящие сигналы для скрытого слоя hidden_outputs = self.activation_function(hidden_inputs) # рассчитать входящие сигналы для выходного слоя final_inputs = numpy.dot(self.who, hidden_outputs) # рассчитать исходящие сигналы для выходного слоя final_outputs = self.activation_function (final_inputs) # ошибки выходного слоя = # (целевое значение - фактическое значение) output_errors = targets - final_outputs # ошибки скрытого слоя - это ошибки output_errors, # распределенные пропорционально весовым коэффициентам связей # и рекомбинированные на скрытых узлах hidden_errors = numpy.dot(self.who.T, output_errors) # обновить весовые коэффициенты для связей между # скрытым и выходным слоями self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose (hidden_outputs)) # обновить весовые коэффициенты для связей между # входным и скрытым слоями self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs)) # опрос нейронной сети def query(self, inputs_list): # преобразовать список входных значений # в двухмерный массив inputs = numpy.array(inputs_list, ndmin=2).T # рассчитать входящие сигналы для скрытого слоя hidden_inputs = numpy.dot(self.wih, inputs) # рассчитать исходящие сигналы для скрытого слоя hidden_outputs = self.activation_function(hidden_inputs) # рассчитать входящие сигналы для выходного слоя final_inputs = numpy.dot(self.who, hidden_outputs) # рассчитать исходящие сигналы для выходного слоя final_outputs = self.асtivation_function(final_inputs) return final_outputs
[In 2]: # количество входных, скрытых и выходных узлов input_nodes = 784 hidden_nodes = 200 output_nodes = 10 # коэффициент обучения learning_rate = 0.01 # создать экземпляр нейронной сети n = neuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)
[In 3]: # загрузить в список тестовый набор данных CSV-файла набора MNIST training_data_file = open("D:/NN/mnist_train.csv", 'r') training_data_list = training_data_file.readlines() training_data_file.close()
[In 4]: # тренировка нейронной сети # переменная epochs указывает, сколько раз тренировочный # набор данных используется для тренировки сети epochs = 10 for е in range(epochs): # перебрать все записи в тренировочном наборе данных for record in training_data_list: # получить список значений, используя символы запятой (',') # в качестве разделителей all_values = record.split(',') # масштабировать и сместить входные значения inputs = (numpy.asfarray(all_values[1:]) / 255 * 0.99) + 0.01 # создать целевые выходные значения (все равны 0,01, за исключением # желаемого маркерного значения, равного 0,99) targets = numpy.zeros(output_nodes) + 0.01 # all_values[0] - целевое маркерное значение для данной записи targets[int(all_values[0])] = 0.99 n.train(inputs, targets) ## создание повернутых вариантов # повернуть против часовой стрелки на x градусов inputs_plusx_img = scipy.ndimage.interpolation.rotate(inputs.reshape(28, 28), 10, cval=0.01, order=1, reshape=False) n.train(inputs_plusx_img.reshape(784), targets) # повернуть по часовой стрелке а x градусов inputs_minusx_img = scipy.ndimage.interpolation.rotate(inputs.reshape(28, 28), -10, cval=0.01, order=1, reshape=False) n.train(inputs_minusx_img.reshape(784), targets)
[In 5]: # загрузить в список тестовый набор данных CSV-файла набора MNIST test_data_file = open("D:/NN/mnist_test.csv", 'r') test_data_list = test_data_file.readlines() test_data_file.close()
[In 6]: # тестирование нейронной сети # журнал оценок работы сети, первоначально пустой scorecard = [] # перебрать все записи в тестовом наборе данных for record in test_data_list: # получить список значений из записи, используя символы # запятой (',') в качестве разделителей all_values = record.split(',') # правильный ответ - первое значение correct_label = int (all_values[0]) # масштабировать и сместить входные значения inputs = (numpy.asfarray(all_values[1:]) / 255 * 0.99) + 0.01 # опрос сети outputs = n.query(inputs) # индекс наибольшего значения является маркерным значением label = numpy.argmax(outputs) # присоединить оценку ответа сети к концу списка if (label == correct_label): # в случае правильного ответа сети присоединить # к списку значение 1 scorecard.append(1) else: # в случае неправильного ответа сети присоединить # к списку значение 0 scorecard.append(0)
[In 7]: # рассчитать показатель эффективности в виде # доли правильных ответов scorecard_array = numpy.asarray(scorecard) print("эффективность = ", scorecard_array.sum() / scorecard_array.size)
Запуск этого кода с использованием коэффициента обучения 0,1 и всего лишь одной тренировочной эпохи дает показатель эффективности, равный 0,9669. Это значительное улучшение по сравнению со значением 0,954, полученным без дополнительных повернутых изображений. Такой показатель уже попадает в число лучших из тех, которые опубликованы на сайте Яна Лекуна (http://yann.lecun.com/exdb/mnist/).
Запустим серию экспериментов, изменяя количество эпох, чтобы проверить, можно ли еще больше улучшить полученный показатель эффективности обучения. Кроме того, уменьшим коэффициент обучения до 0,01, поскольку, предоставив гораздо больше тренировочных данных и тем самым увеличив общее время обучения, мы можем позволить себе более осторожные шаги обучения меньшей величины.
Не забывайте о том, что мы не ожидаем получить точность распознавания 100%, поскольку, вероятно, существует естественный предел точности, обусловленный спецификой архитектуры нейронной сети или полнотой тренировочных данных, в связи с чем мы вряд ли можем получить точность выше примерно 98%. Под "спецификой архитектуры нейронной сети" здесь подразумевается выбор количества узлов в каждом слое, количества скрытых слоев, функции активации и т.п.
Ниже представлены графики, отражающие зависимость эффективности нейронной сети от угла поворота дополнительных тренировочных изображений. Для сравнения показана также точка данных, соответствующая отсутствию дополнительных примеров.
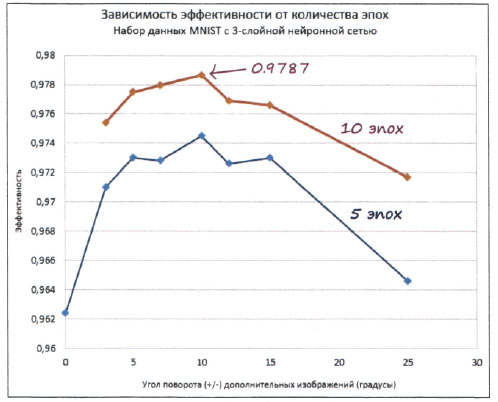
Как видите, для пяти эпох наилучший результат равен 0,9745, или 97,5% точности. Это явное улучшение по сравнению с предыдущим примером.
Также следует отметить, что с увеличением угла поворота изображения точность падает. Это вполне объяснимо, поскольку при больших углах поворота результирующие изображения фактически вообще не представляют цифры. Представьте цифру "3", повернутую на 90 градусов, т.е. положенную на бок. Это будет вовсе не тройка. Поэтому, добавляя тренировочные примеры с чрезмерно большими углами поворота, мы снижаем качество тренировки, потому что добавляемые примеры являются ложными. Пожалуй, оптимальным углом поворота для дополнительных тренировочных изображений является угол 10 градусов.
Для десяти эпох рекордное пиковое значение точности составляет 0,9787, или почти 98%! Это поистине ошеломляющий результат для простой нейронной сети такого рода. Не забывайте о том, что мы не использовали никаких изощренных математических трюков в отношении нейронной сети или данных, как это делают некоторые люди. Мы придерживались предельной простоты и тем не менее достигли результатов, которыми по праву можем гордиться.

Отличная работа!
На следующем шаге мы подведем итог изученному материалу.
