На этом шаге мы рассмотрим дифференцирование более сложных функций.
Представьте, что в функции
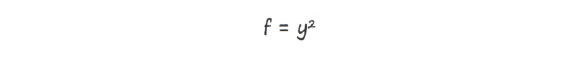
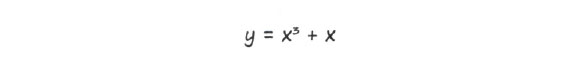
При желании можно переписать эту формулу в виде f = (х8 + х)2.
Как f изменяется с изменением у? То есть что собой представляет производная df / dy? Получить ответ на этот вопрос не составляет труда, поскольку для этого достаточно применить только что полученное нами правило дифференцирования степенных выражений, поэтому df / dy = 2у.
Но возникает более интересный вопрос: как изменяется f при изменении х? Ну хорошо, мы могли бы раскрыть выражение f = (х8 + х)2 и применить уже знакомый подход. Только ни в коем случае не считайте наивно, что производная от (х8 + х)2 - это 2(х8 + х).
Если бы мы проделали множество подобных вычислений прежним трудоемким способом, предполагающим устремление приращений к нулю в результирующих выражениях, то рано или поздно мы подметили бы еще одну закономерность. Дадим вам сразу же готовый рецепт.
Вот как выглядит новая закономерность.
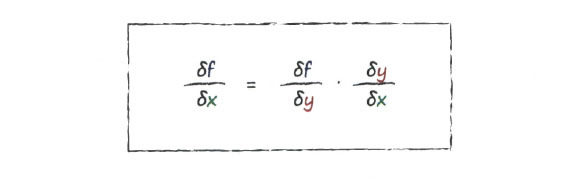
Это очень мощный результат, который называется цепным правилом.
В соответствии с этим правилом нахождение производной в подобных случаях осуществляется поэтапно. Может оказаться так, что для нахождения производной df / dx проще найти производные df / dy и dy / dx. Если последние две производные действительно вычисляются очень просто, то с помощью этого приема удается находить производные, определить которые другими способами практически невозможно. Цепное правило позволяет разбивать трудные задачи на более легкие.
Рассмотрим следующий пример и применим к нему цепное правило:
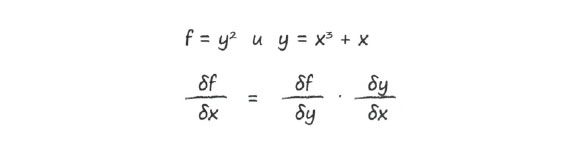
Мы разбили задачу на две простые части. Первая часть дает (df / dy) = 2у, вторая - (dy / dx) = Зх2 + 1. Объединяя эти части с помощью цепного правила, получаем
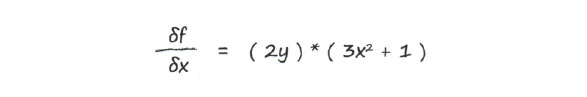
Мы знаем, что у = х3 + х, поэтому можем получить выражение, содержащее только х:
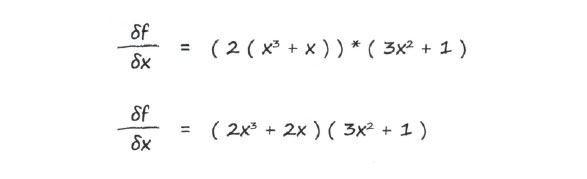
Магия!
Возможно, вас так и подмывает спросить: а почему бы не представить f в виде функции, зависящей только от х, и применить простое правило дифференцирования степеней к результирующему полиному? Мы могли бы это сделать, но тогда мы не продемонстрировали бы вам, как работает цепное правило, которое позволяет разгрызать более твердые орешки.
Рассмотрим еще один пример, на этот раз последний, который демонстрирует, как обращаться с переменными, не зависящими от других переменных.
Предположим, имеется функция
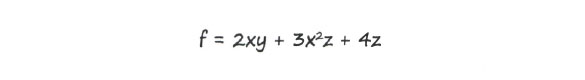
В ней переменные х, у и z не зависят одна от другой. Что мы подразумеваем под независимостью переменных? Под этим подразумевается, что каждая из переменных х, у и z может принимать любые значения, какими бы ни были значения остальных переменных - их изменения на нее не влияют. В предыдущем примере это было не так, поскольку значение у определялось значением выражения х8 + х, а значит, переменная у зависела от х.
Что такое df / dx? Рассмотрим каждый член длинного полинома по отдельности. Первый член - это 2ху, поэтому его производная равна 2у. Почему так просто? Да потому, что у не зависит от х. Когда мы интересуемся величиной df / dx, нас интересует, как изменяется f при изменении х. Если переменная у не зависит от х, то с ней можно обращаться как с константой. На ее месте могло бы быть любое другое число, например 2, 3 или 10.
Идем дальше. Следующий член выражения - 3x2z. Применяя правило понижения степеней, получаем 2*3xz или 6xz. Мы рассматриваем z как обычную константу, значением которой может быть 2, 4 или 100, поскольку х и z не зависят друг от друга. Изменение z не влияет на х.
Последний член, 4z, вообще не содержит х. Поэтому он полностью исчезает, так как мы рассматриваем его как постоянное число, которым, например, могло бы быть 2 или 4.
Вот как выглядит окончательный ответ:
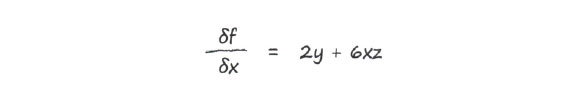
В этом примере была важна возможность уверенно игнорировать переменные, о которых известно, что они являются независимыми. Это значительно упрощает дифференцирование довольно сложных выражений, в чем часто возникает необходимость в ходе анализа нейронных сетей.
На следующем шаге мы подведем некоторые итоги.
