На этом шаге мы выявим некоторые закономерности, которые помогут нам в вычислениях.
Конечно, это весьма интересное занятие - находить производные, используя приращения наподобие Δх, и смотреть, что произойдет, если делать их все меньшими и меньшими. Но зачастую можно получить результат, не выполняя всю эту работу.
Посмотрите на приведенные ниже формулы и постарайтесь увидеть в них закономерность.
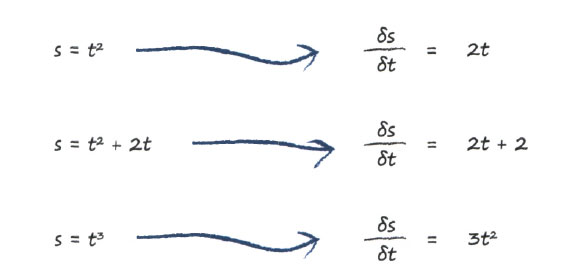
Вы видите, что производная функции t представляет собой ту же функцию, но с понижением на единицу каждой степени t. Поэтому t4 превращается в t3, a t7 превратилось бы в t6 и т.д. Это очень просто! А если вы вспомните, что t - это t1, то в производной это превращается в t0, т.е. в 1.
Свободные постоянные члены, такие как 3, 4 или 5, просто исчезают. Постоянные переменные, не являющиеся коэффициентами, такие как а, b или с, также исчезают, поскольку скорость их изменения также нулевая. Именно поэтому их называют константами.
Но погодите, ведь t2 превращается в 2t, а не просто в t, a t3 превращается в 3t2, а не просто в t2. Это общее правило: степень переменной, прежде чем уменьшиться на единицу, становится коэффициентом.
Поэтому 5 в 2t5 используется в качестве дополнительного коэффициента перед уменьшением степени на единицу: 5 * 2t4 = 10t4.
Приведенная ниже формула суммирует все, что было сказано о дифференцировании степеней, в виде следующего правила:

Испытаем эту формулу на дополнительных примерах только ради того, чтобы набить руку в использовании этого нового приема:
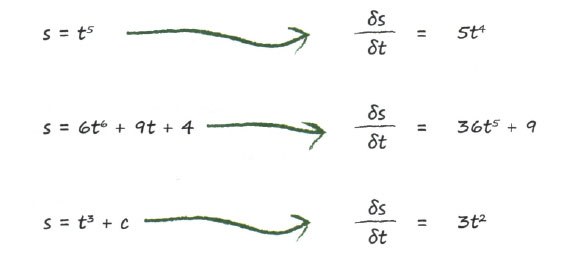
Это правило пригодится вам во многих случаях, а зачастую ничего другого вам и не потребуется. Верно и то, что правило применимо только к полиномам, т.е. к выражениям, состоящим из переменных в различных степенях, как, например, выражение у = ах8 + bx2 + сх + d, но не к функциям вида sin(x) или соs(х). Это не является существенным недостатком, поскольку в огромном количестве случаев вам вполне хватит правила дифференцирования степеней.
Однако для нейронных сетей нам понадобится еще один инструмент, о котором сейчас пойдет речь.
На следующем шаге мы рассмотрим функции функций.
