На этом шаге мы приведем еще несколько примеров рекурсии.

Ещё одна функция, которая может быть выражена рекурсивно, - это факториал некоторого неотрицательного целого числа n:

   n! = 1 * 2 * ... * (n - 1) * n    .

В этом случае рекурсивность функции не столь очевидна из-за явного отсутствия в правой части определения факториала. Но поскольку (

   (n - 1)! = 1 * 2 * ... * (n - 1)               ,

можно переписать формулу рекурсивно:

    n! = (n - 1)! * n              .

Наконец, по определению 0! = 1, что следует из рекурсивной формулы для n = 1. Таким образом, функция факториала может быть определена рекурсивно как

      1, если n = 0
n! =                                        (1.3)
      (n - 1)! * n, если n > 0

Рассмотрим также задачу вычисления суммы первых n положительных целых чисел. Соответствующая функция S(n) может быть, очевидно, определена как:

    S(n) = 1 + 2 + ... + (n - 1) + n.       (1.4)

И снова мы пока не видим в правой части определения слагаемого, содержащего функцию S. Однако первые n - 1 членов можно сгруппировать так, чтобы получить

    S(n - 1) = 1 + 2 + ... + (n - 1)          ,

что приводит к следующему рекурсивному определению:

        1, если n = 1
S(n) =                                      (1.5)
        S(n - 1) + n, если n > 1

Отметим, что S(n - 1) - подзадача, подобная S(n), но более простая, так как для получения её результата требуется меньшее количество операций. Таким образом, говорят, что подзадача имеет меньший размер (размерность). Кроме того, мы говорим, что выполнена декомпозиция (разложение) исходной задачи (S(n)) на меньшие для формирования рекурсивного определения. Таким образом, S(n - 1) - меньший экземпляр исходной задачи.

Другой математический объект, рекурсивность которого не вполне очевидна, - неотрицательные целые числа. Эти числа можно разложить и определить рекурсивно через меньшие числа разными способами. Например, неотрицательное целое число n можно представить как предшествующее ему число плюс один:

     0, если n = 0
n = 
     predesessor(n) + 1, если n > 0

Заметим, что в рекурсивном условии n находится по обе стороны от знака равенства. Кроме того, если мы считаем, что функция predecessor() обязательно возвращает неотрицательное целое число, то она неприменима к 0. Поэтому определение становится законченным только вместе с тривиальным начальным условием для n = 0.

Ещё один способ определения (неотрицательных) целых чисел - считать их упорядоченной последовательностью цифр. Например, число 5342 может быть конкатенацией следующих пар меньших чисел:

    (5, 342), (53, 42), (534, 2).

На практике простейший способ декомпозиции целого числа - это представление его в виде соединения наименьшей его значащей цифры с остальной его частью. Поэтому целое число можно определить следующим образом:

     n, если n < 10
n = 
     (n // 10) * 10 + (n % 10), если n >= 10

где // и % - операции вычисления частного и остатка целочисленного деления соответственно, в обозначениях языка Python. Например, если n = 5342, то частное (n // 10) = 534, а остаток (n % 10) = 2 - наименьшая значащая цифра n. Понятно, что само число n можно восстановить, умножив частное на 10 и добавив к полученному результату остаток. Начальное условие имеет дело только с однозначными числами, которые, конечно же, не могут быть подвержены разложению.

Математика просто изобилует рекурсивными выражениями. Так, например, они часто используются для описания свойств функций. Следующее рекурсивное выражение говорит о том, что производная суммы функций есть сумма её производных:

    [fx) + g(x)]' = [f(x)]' + [g(x)]'                 .

В этом случае рекурсивный объект - это производная функции, обозначаемая как [-]', но не сами функции f(x) и g(x). Заметьте, что формула явно указывает на имеющую место декомпозицию, где некоторая первичная функция (являющаяся входным параметром производной функции) разложена на сумму функций f(x) и g(x).

Структуры данных тоже можно считать рекурсивными объектами. На рисунке 1 показано, как могут быть подвергнуты рекурсивной декомпозиции структуры данных список и дерево.

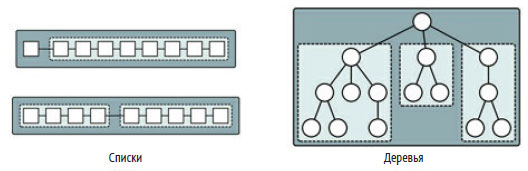
Рис.1. Рекурсивная декомпозиция списков и деревьев

Список может состоять из одного элемента плюс ещё список (это обычное определение списка как абстрактного типа данных). Или же он может быть поделён на несколько списков (в этом, более широком контексте список - это любая коллекция элементов данных, которые линейно упорядочены в определённой последовательности, как в списках, массивах, кортежах и т. д.). Дерево же состоит из родительской вершины и множества (или списка) поддеревьев, корневой узел которых - прямой потомок исходной родительской вершины. Рекурсивные определения структур данных заканчиваются пустыми (начальными) значениями. Например, список из одного элемента мог бы состоять из этого элемента плюс пустой список. Наконец, обратите внимание, что в этих схемах более темные поля представляют рекурсивный объект в целом, тогда как светлые обозначают меньшие и подобные ему экземпляры.

Рекурсия может также использоваться для определения слов в словарях. Это может показаться невозможным, так как нас учат в школе, что толкование слова в словаре не может содержать внутри себя это же слово. Однако многие понятия могут быть определены правильно именно так. Рассмотрим термин "потомок" определенного предка. Обратите внимание, что он может быть определён так: некто, являющийся либо ребёнком своего предка, либо потомком любого из детей своего предка. В этом случае мы можем определить рекурсивную конструкцию, в которой множество потомков можно представить (генеалогическим) древом, как на рисунке 2, где тёмные блоки содержат всех потомков общего предка (корня дерева), а светлые - потомков детей предка.

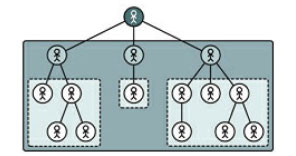
Рис.2. Генеалогическое древо потомков человека - его детей и потомков их детей

На следующем шаге мы рассмотрим декомпозицию задачи.

Предыдущий шаг Содержание Следующий шаг