На этом шаге мы приведем пример декомпозиции.

Вообще говоря, основная задача рекурсивного мышления и программирования - дать наши собственные рекурсивные определения объектам, понятиям, функциям, задачам и т. д. И если первый шаг обычно сводится к выявлению начальных условий, то главная задача состоит в определении рекурсивных условий. В связи с этим важно усвоить понятия

(a) декомпозиции задачи и
(b) индукции,

которые мы вкратце рассмотрим в следующих шагах.

Наша цель будет заключаться в разработке рекурсивных алгоритмов решения вычислительных задач. Их следует понимать как вопросы, на которые могут ответить компьютеры и которые задаются в виде высказываний, описывающих отношения между заданным набором входных значений или параметров и множеством выходных значений, результатов или решений. Например: "Дано некое положительное целое число n. Найти сумму первых n положительных целых чисел" - это формулировка вычислительной задачи с одним входным параметром (n) и одним выходным значением, определяемым как

   1 + 2 + ... + (n - 1) + n  .

Экземпляр задачи - это определённый набор допустимых входных значений, которые позволяют нам получить решение задачи. Тогда как алгоритм - это логическая процедура, определяющая пошаговый процесс вычислений для получения по заданным входным значениям выходных значений. Таким образом, алгоритм определяет, как решить задачу. Заслуживает внимания то, что вычислительные задачи могут решаться различными алгоритмами. Цель состоит в том, чтобы объяснить, как разработать и реализовать рекурсивные алгоритмы и программы, где основным этапом является декомпозиция вычислительной задачи.

Декомпозиция - важное понятие в информатике, играющее главную роль не только в рекурсивном программировании, но и в решении задач вообще. Суть её состоит в разложении сложной задачи на меньшие и более простые подзадачи, которые проще выразить, вычислить, закодировать и решить. После чего решения подзадач используются для получения решения более сложной исходной задачи.

В контексте рекурсивного решения задач и программирования декомпозиция подразумевает разложение вычислительной задачи на несколько подзадач, некоторые из которых подобны исходной, как показано на рисунке 1.

Рис.1. Рекурсивное решение задачи

Отметим, что для решения задачи может потребоваться решение других, дополнительных задач, которые не являются подобными исходной. Здесь будет несколько таких задач, но в этих вводных шагах мы приведём только такие примеры, где исходные задачи разбиваются только на себе подобные.

В качестве первого примера снова рассмотрим задачу вычисления суммы первых n положительных целых чисел, обозначаемой как S(n) и выраженной формулой (1.4). Есть несколько способов разбить задачу на меньшие подзадачи и сформировать рекурсивное определение S(n). Во-первых, она зависит только от входного параметра n, который определяет также размер задачи. В этом примере начальное условие связано с наименьшим целым положительным числом n = 1, и очевидно, что S(1) = 1 - наименьший экземпляр задачи. В дальнейшем при рассмотрении подзадач нам, возможно, придётся уточнить начальное условие задачи. Поэтому мы должны подумать, каким образом мы будем уменьшать размер задачи - входной параметр n.

Первый вариант - уменьшать n на единицу. В этом случае наша цель - определить S(n), используя подзадачу S(n - 1). Соответствующее рекурсивное решение, полученное алгебраически, приведено в (1.5). Рекурсивное условие можно также вывести из графического представления задачи. Например, можно подсчитать общее число блоков в "треугольной" пирамиде, которая содержит n блоков в первом (нижнем) своём ряду, n - 1 - во втором и т. д. (верхний n-й ряд состоит только из одного блока), как показано на рисунке 2(a) для n = 8.

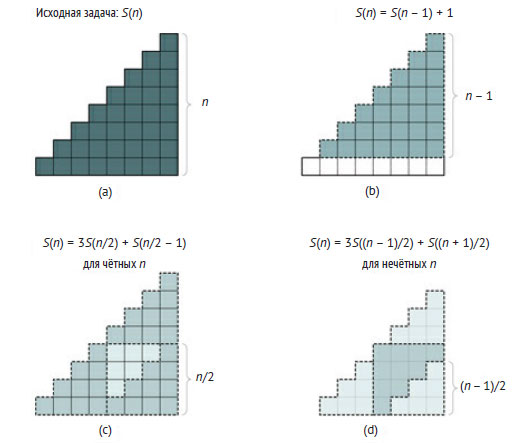
Рис.2. Декомпозиции суммы первых положительных целых чисел

Для рекурсивной декомпозиции задачи нам нужно найти подобные ей задачи. В этом случае нетрудно найти в исходном треугольнике меньшие подобные треугольники. Например, на рисунке 2(b) показан треугольник высотой n - 1, включающий все блоки исходного треугольника, за исключением n блоков первого ряда. Поскольку этот меньший треугольник содержит ровно S(n - 1) блоков, из этого следует, что S(n) = S(n - 1) + n.

Другой вариант декомпозиции с подзадачей суммирования n - 1 членов заключается в рассмотрении суммы

    2 + ... + (n - 1) + n.

Однако тут важно отметить, что эта задача не подобна S(n). Очевидно, что это не сумма первых положительных целых чисел, а частный случай более общей задачи суммирования всех целых чисел от некоторого начального значения m до некоторого большего значения n:

    m + (m + 1) + ... + (n - 1) + n, где m < n.

Различие между обеими задачами можно также пояснить графически. На рисунке 2 этой общей задаче соответствовал бы прямой трапециоид треугольника. В итоге можно вычислить сумму первых n положительных целых чисел, используя эту, более общую задачу, если задать m = 1. Однако её рекурсивное определение сложнее, так как требует вместо одного два входных параметра m и n.

Другие варианты декомпозиции этой задачи состоят в том, чтобы уменьшать n с шагом, большим 1. Например, все входные значения n можно разбить на чётные и нечётные, чтобы получить декомпозицию, приведённую на рисунках 2(c) и 2(d). Если n - чётное, то внутри большого треугольника, соответствующего S(n), можно разместить три треугольника высотой n/2. И поскольку оставшийся блок - тоже треугольник высотой n/2 - 1, рекурсивную формулу можно записать как

    S(n) = 3S(n/2) + S(n/2 - 1)   .

С другой стороны, если n - нечётное, то внутри треугольника можно разместить три треугольника высотой (n - 1)/2 и один высотой (n + 1)/2. Так что в этом случае рекурсивная формула примет вид

    S(n) = 3S((n - 1)/2) + S((n + 1)/2)     .

Окончательная рекурсивная функция:


        1,                             если n = 1
        2,                             если n = 2
S(n) =                                                                (1.6)
        3S(n/2) + S(n/2 - 1),          если n > 2 и n - четное,
        3S((n - 1)/2) + S((n + 1)/2),  если n > 2 и n - нечетное,

Важно отметить, что определение нуждается в дополнительном начальном условии для n = 2. Иначе в рекурсивном условии для чётных n мы получили бы

    S(2) = 3S(1) + S(0)              .

Но по условию задачи S(0) не определена, поскольку входными значениями для S должны быть только положительные целые числа. Таким образом, новое начальное условие исключает применение рекурсивной формулы для n = 2.

За счёт уменьшения размера задачи её подзадачи становятся значительно меньше исходной и потому могут решаться намного быстрее. Грубо говоря, если число подзадач, которые должны быть решены, мало и существует возможность разумного объединения их решений, то такая стратегия может привести к существенно более быстрым алгоритмам решения исходной задачи. Однако в этом частном примере код для (1.6) не обязательно эффективнее кода для (1.5). Интуитивно потому, что (1.6) требует решения двух подзадач (с различными параметрами), тогда как (1.5) содержит только одну подзадачу. Оценку стоимости выполнения рекурсивных алгоритмов мы рассмотрим позже.

На следующем шаге мы закончим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг