На этом шаге мы приведем еще несколько рекурсивных задач.

В последнем способе суммирования первых n положительных целых чисел исходная задача делилась на две подзадачи меньшего размера, где новые входные параметры удовлетворяют заданным начальным условиям. В самом общем случае можно разбивать задачи на любое количество более простых подзадач до тех пор, пока новые параметры тесно связаны со значениями, заданными в начальных условиях. Например, рассмотрим следующее альтернативное рекурсивное определение функции Фибоначчи (эквивалент (1.2)):

        1,          если n = 1
F(n) =  1,          если n = 2                          (1.7)
           _n-2
        1 + ∑ F(i), если n > 2
           ⁱ⁼¹

где ∑^n-2_i=1F(i) есть сумма F(1) + F(2) + ... + F(n - 2). В этом примере для некоторого значения n размера исходной задачи рекурсивное условие использует результаты всех меньших подзадач размером от 1 до n - 2.

В последнем примере декомпозиции задачи мы будем использовать списки, которые позволят нам обращаться к отдельным его элементам посредством числовых индексов (во многих языках программирования такую структуру данных называют "массивом", тогда как в Python это просто "список"). Задача заключается в суммировании значений элементов списка, обозначаемого как a и содержащего n чисел. Формально задача может быть записана как:

      _n-1
s(a) = ∑ a[i] = a[0] + a[1] + ... + a[n - 1],     (1.8)
      _i=0

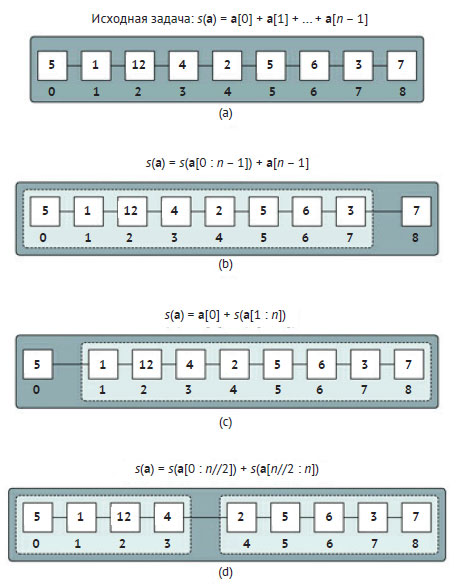
где a[i] - (i + 1)-й элемент списка, поскольку 1-й элемент списка имеет индекс 0. На рисунке 1(a) изображён частный случай списка из 9 элементов.

Рис.1. Декомпозиции суммы элементов списка a из n = 9 чисел

Что касается обозначений, то мы будем считать, что подсписок некоторого списка a - это коллекция смежных элементов a, если явно не оговаривается иное. Напротив, в подпоследовательности некоторой последовательности s её элементы появляются в том же порядке, что и в s, но они не обязаны быть смежными. Другими словами, подпоследовательность может быть получена из исходной последовательности s удалением некоторых элементов s без изменения порядка следования оставшихся элементов.

Декомпозиция задачи заключается в уменьшении её размера на единицу. С одной стороны, список можно разбить на подсписок из первых n - 1 элементов (a[0:n - 2], где a[i:j] - подсписок от a[i] до a[j - 1] в обозначениях языка Python) и единственный элемент (a[n - 1]), соответствующий последнему числу в списке (рисунок 1(b)). В этом случае задачу можно определить рекурсивно таким образом:

       0,                        если n = 0,
s(a) =                                            (1.9)
       s(a[0:n - 2]) + a[n - 1], если n > 0.

В рекурсивном условии подзадача решается, естественно, для подсписка размером n - 1. Начальное условие рассматривает тривиальную ситуацию, когда список пуст и совсем не требует суммирования.

Вторым возможным начальным условием может быть s(a) = a[0] для n = 1. Однако оно было бы избыточным при такой декомпозиции и поэтому не обязательно. Обратите внимание, что при n = 1 функция добавляет a[0] к нулевому результату применения функции к пустому списку. Таким образом, второе начальное условие можно опустить для краткости.

С другой стороны, исходный список можно также представить как его первый элемент a[0] и меньший список a[1:n] (см. рисунок 1(c)). В этом случае задача может быть записана рекурсивно как:

        0,                если n = 0,
s(a) =                                              (1.10)
        a[0] + s(a[1:n]), если n > 0.

Хотя обе декомпозиции очень похожи, код для каждой из них может весьма отличаться в разных языках программирования. В дальнейших шагах мы приведём несколько способов кодирования алгоритма решения задачи для каждой из этих декомпозиций.

Ещё один способ декомпозиции задачи - деление списка пополам, как на рисунке 1(d). Это приводит к двум подзадачам размером примерно в половину исходной. Декомпозиция даёт следующее рекурсивное определение:

        0,                          если n = 0,
s(a) =  a[0],                       если n = 1,        (1.11)
        s(a[0:n//2] + s(a[n//2:n]), если n > 1.

В отличие от предыдущих определений такая декомпозиция требует начального условия для n = 1. Без него функция никогда бы не вернула конкретного значения для непустого списка. Обратите внимание, что такое определение не складывало бы и не возвращало ни одного элемента списка. Для непустого списка рекурсивное условие применялось бы многократно, и этот процесс никогда бы не закончился. Такая ситуация называется бесконечной рекурсией. Например, если бы список содержал только один элемент, то рекурсивное условие добавило бы значение 0, соответствующее пустому списку, к результату такой же исходной задачи. Иными словами, мы пытались бы бесконечно вычислить

    s(a) = 0 + s(a) = 0 + s(a) = 0 + s(a) + ...     .

Очевидная проблема такого сценария - в том, что при n = 1 исходная задача s(a) уже не может быть разбита на меньшие и более простые.

На следующем шаге мы рассмотрим рекурсивный код.

Предыдущий шаг Содержание Следующий шаг