На этом шаге мы рассмотрим более сложные примеры рекурсии.

    Для более сложных типов данных различий в кодах разных языков программирования может становиться ещё больше из-за низкоуровневых деталей. Например, при работе с такой структурой данных, как список, рекурсивным алгоритмам для вычленения подсписков нужно знать его длину. На рисунке 1 приведены три варианта списков (или подобных им структур данных) с параметрами, необходимыми для вычленения подсписков в рекурсивных программах.

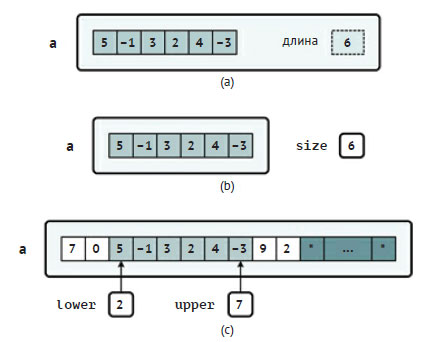
Рис.1. Списочные структуры данных с параметрами, необходимыми для определения подсписков

    В случае (a) длина списка a может быть получена без использования дополнительных переменных или параметров. Например, она может быть свойством или методом списка. В языке Python длину списка можно получить вызовом функции len(). Однако в таких языках программирования, как C или Паскаль, получить длину стандартного массива невозможно. Если длину списка нельзя извлечь непосредственно из структуры данных, то для хранения и получения длины списка нужен дополнительный параметр, например size, как в случае (b). Такой подход может применяться при работе с массивами - фиксированного размера или частично заполненными. Правда, в подобных случаях лучше использовать начальный и конечный индексы, задающие границы подсписка, как в случае (c). Отметим, что в этом случае фиксированный размер структуры данных может быть довольно большим (достаточным для нужд приложения), хотя истинная длина списков и подсписков может быть гораздо меньше. На рис. 1(c) изображён список, использующий только первые 10 элементов (остальные игнорируются). Внутри него определён подсписок из шести элементов с нижней (lower) и верхней (upper) индексными переменными, ограничивающими его пределы. Отметим, что элементы с этими индексами входят в подсписок.

    Конструкции и синтаксис языка Python поддерживают высокий уровень алгоритмизации задач, избегая необходимости знать механизмы нижнего уровня, такие, например, как передача параметров. Однако его гибкость допускает большое разнообразие возможностей кодирования. В примере 1.5 приводятся три решения задачи суммирования элементов списка, соответствующих трём способам декомпозиции на рисунке 1 5 шага, в которых единственным входным параметром является список, изображённый на рисунке 1(a).

    Функции sum_list_length_1(), sum_list_length_2() и sum_list_ length_3() реализуют рекурсивные определения (1.9), (1.10) и (1.11) соответственно. Заключительные строки примера объявляют список a и печатают сумму его элементов, используя эти три функции. Отметим, что количество элементов n списка вычисляется функцией len(). В заключение напомним, что a[lower:upper] - это подсписок a от индекса lower до upper - 1, тогда как [lower:] равносильно [lower:len(a)]. Если размер списка нельзя получить непосредственно из списка, то его можно передать дополнительным параметром функции, как показано на рисунке 1(b). Соответствующий код подобен примеру 1.5.

    В примере 1.6 приводится другой вариант тех же функций с использованием больших списков и двух параметров (lower и upper), определяющих подсписки внутри этого списка, как показано на рис. 1(c).

    Обратите внимание на аналогию этих функций с функциями из примера 1.5. В данном случае список пуст, когда lower больше upper. Кроме того, подсписок содержит единственный элемент, если значения обоих индексов совпадают (напомним, что оба параметра указывают позиции элементов, входящих в подсписок).

# Decomposition: s(a) => s(a[0:n-1]), a[n-1]
def sum_list_length_1(a):
    if len(a) == 0:
        return 0
    else:
        return (sum_list_length_1(a[0:len(a) - 1])
                + a[len(a) - 1])


# Decomposition: s(a) => a[0], s(a[1:n])
def sum_list_length_2(a):
    if len(a) == 0:
        return 0
    else:
        return a[0] + sum_list_length_2(a[1:len(a)])


# Decomposition: s(a) => s(a[0:n//2]), s(a[n//2:n])
def sum_list_length_3(a):
    if len(a) == 0:
        return 0
    elif len(a) == 1:
        return a[0]
    else:
        middle = len(a) // 2
        return (sum_list_length_3(a[0:middle])  
                + sum_list_length_3(a[middle:len(a)]))  


# Some list:
a = [5, -1, 3, 2, 4, -3]

# Function calls:
print(sum_list_length_1(a))
print(sum_list_length_2(a))
print(sum_list_length_3(a))

# Decomposition: s(a) => s(a[0:n-1]), a[n-1]
def sum_list_limits_1(a, lower, upper):
    if lower > upper:
        return 0
    else:
        return a[upper] + sum_list_limits_1(a, lower, upper - 1)  


# Decomposition: s(a) => a[0], s(a[1:n])
def sum_list_limits_2(a, lower, upper):
    if lower > upper:
        return 0
    else:
        return a[lower] + sum_list_limits_2(a, lower + 1, upper)


# Decomposition: s(a) => s(a[0:n//2]), s(a[n//2:n])
def sum_list_limits_3(a, lower, upper):
    if lower > upper:
        return 0
    elif lower == upper:
        return a[lower]  # or a[upper]
    else:
        middle = (upper + lower) // 2
        return sum_list_limits_3(a, lower, middle) \
               + sum_list_limits_3(a, middle + 1, upper)


# Some list:
a = [5, -1, 3, 2, 4, -3]

# Function calls:
print(sum_list_limits_1(a, 0, len(a) - 1))
print(sum_list_limits_2(a, 0, len(a) - 1))
print(sum_list_limits_3(a, 0, len(a) - 1))

    Со следующего шага мы начнем знакомиться с индукцией.

Предыдущий шаг Содержание Следующий шаг