На этом шаге мы рассмотрим использование процедур при разработке рекурсивных алгоритмов.

    До сих пор нам могло показаться, что если результат определяется формулой, то методу всегда соответствует функция, возвращающая значение. И потому он может использоваться в выражениях других методов, куда возвращает определённое значение от заданных входных параметров. Однако в некоторых языках программирования (например, в Паскале) существуют методы, называемые "процедурами", которые не возвращают значений. Вместо этого они могут изменять структуры данных, передаваемые методу в качестве аргументов, или просто отображать некоторую информацию на экране. Оказывается, что и в таких случаях также можно пользоваться общей схемой декомпозиции задачи.

    Рассмотрим задачу вывода на экран цифр некоторого неотрицательного целого числа n - по вертикали и в обратном порядке. То есть наименьшая значащая цифра должна появиться в 1-й строке, следующая - во 2-й и т. д. Например, если n = 2743, программа должна вывести на экран следующие строки:

    Во-первых, размер этой задачи - количество цифр в числе n. Начальное условие выполняется, когда n состоит из одной цифры (n < 10), и алгоритм просто должен вывести n. Как в предыдущем примере, самая простая декомпозиция рассматривает n//10 с отбрасыванием из исходного числа наименьшей значащей цифры. На рисунке 1 показана возможная схема декомпозиции задачи.

Рис.1. Схема декомпозиции задачи вывода на экран цифр неотрицательного целого числа - вертикально и в обратном порядке: (a) - частный случай (n = 2743), (b) - общий случай числа из m цифр (n = d_m-1 ... d₁d₀)

    Кроме того, для такого типа процедур также применима общая схема:

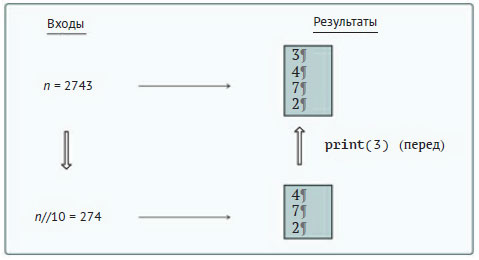
    В этом примере результатом являются не столько сами числовые значения, сколько последовательность команд вывода строк на экран. Для такой задачи решением будет вывод на экран наименьшей значащей цифры исходного числа с последующим рекурсивным вызовом метода для оставшихся цифр. При этом крайне важна последовательность выполнения этих операций. В частности, наименьшая значащая цифра должна быть выведена до вывода остальных. Соответствующий код приведён в примере 2.3.

def print_digits_reversed_vertically(n):
    if n < 10:
        print(n)
    else:
        print(n % 10)
        print_digits_reversed_vertically(n // 10)  

    На следующем шаге мы рассмотрим несколько подзадач.

Предыдущий шаг Содержание Следующий шаг