На этом шаге мы рассмотрим способ разбиения задачи на несколько подзадач.

    Некоторые алгоритмы требуют разбиения исходной задачи на несколько подобных ей подзадач, а процесс осмысления рекурсивных условий подобен изображённому на рисунке 1 25 шага. Как показано на рисунке 1, схемы просто должны включать различные подзадачи и соответствующие им решения согласно выбранной декомпозиции. В таких случаях, помимо расширения и изменения решения каждой из подзадач, рекурсивные условия обычно должны ещё и объединять их.

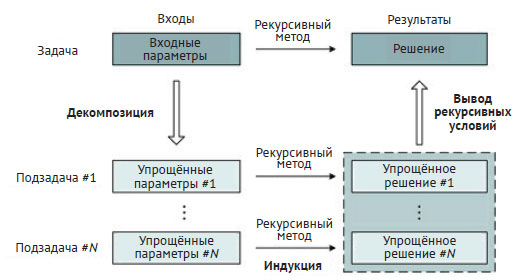
Рис.1. Общая схема осмысления рекурсивных условий, когда задача разбивается на несколько (N) себе подобных подзадач

    Для заданного непустого списка из n целых чисел (n > 1) рассмотрим задачу поиска в нём наибольшего значения. В этом примере мы разделим размер задачи пополам так, чтобы работать с одной и с другой половинами списка, как показано на рисунке 1(d) 5 шага. Следующая схема иллюстрирует процесс осмысления задачи на конкретном примере:

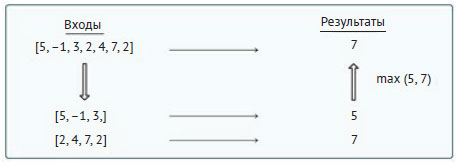
    Толстые и тонкие стрелки обозначают решения задач и подзадач, соответственно.

    На рисунке 2 представлена альтернативная схема декомпозиции и процесс рекурсивного осмысления задачи.

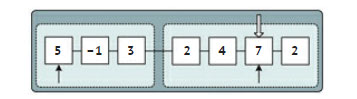
Рис.2. Альтернативная схема декомпозиции методом «разделяй и властвуй» и процесс осмысления задачи поиска наибольшего значения в списке.

    В каждом из вариантов рекурсивный вызов возвращает наибольшее значение в каждой половине. Поэтому рекурсивное условие может возвращать просто максимальное значение из двух половин. Рекурсивная функция f() определена следующим образом:

        a[0],                           если n = 1
f(a) =                                                  (2.3)
        max(f(a[0:n//2]), f(a[n//2:n]), если n > 1

    В примере 2.4 приводятся два способа кодирования функции. Версия, использующая границы lower и upper, обычно быстрее. Конечно, эта задача допускает также рекурсивные решения на основе единственной подзадачи, размер которой уменьшается на 1. Этот подход столь же эффективен, как метод "разделяй и властвуй", но на практике может привести к ошибкам времени выполнения программы для больших списков.

def max_list_length_DaC(a):
    if len(a) == 1:
        return a[0]
    else:
        middle = len(a) // 2
        m1 = max_list_length_DaC(a[0:middle])
        m2 = max_list_length_DaC(a[middle:len(a)])
        return max(m1, m2)


def max_list_limits_DaC(a, lower, upper):
    if lower == upper:
        return a[lower]  # or a[upper]
    else:
        middle = (upper + lower) // 2
        m1 = max_list_limits_DaC(a, 0, middle)
        m2 = max_list_limits_DaC(a, middle + 1, upper)  
        return max(m1, m2)


# Some list:
v = [5, -1, 3, 2, 4, 7, 2]

# Function calls:
print(max_list_length_DaC(v))
print(max_list_limits_DaC(v, 0, len(v) - 1))

    На следующем шаге мы рассмотрим тестирование.

Предыдущий шаг Содержание Следующий шаг