На этом шаге мы напомним основные операции с матрицами и векторами.

Матрица - прямоугольная таблица из чисел (или элементов других типов данных - символьных, логических и т. д.), состоящая из строк и столбцов. Формально матрица A размерности n*m содержит n строк и m столбцов чисел, где n ≥ 1 и m ≥ 1. Обычно матрицы заключаются в квадратные или круглые скобки:

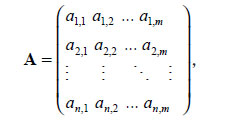
где a_ij обозначает отдельный элемент матрицы A или вход в неё по строке i и столбцу j.

Если одна из размерностей равна 1, то такой математический объект называют вектором. Если же обе размерности равны 1, то объект становится скаляром, то есть числом.

Результатом транспонирования матрицы A размерности n*m является матрица A^T размерности m*n, строками которой выступают столбцы матрицы A (а столбцами - строки A). Например, если

Матрицы (и векторы) можно складывать и умножать. Сумма A + B - это матрица, элементы которой равны a_i,j + b_i,j. Иными словами, матрицы (и векторы) складываются поэлементно. Поэтому A и B должны иметь одинаковую размерность. Типичный пример суммы векторов:

  (4, -1, 2) + (2, 3, -7) = (6, 2, -5).

Умножение матриц гораздо сложнее сложения. Пусть а и b - два n-мерных вектора (столбца). Их скалярное произведение a^Tb (в других обозначениях - a⋅b или (a,b)) - определяется как сумма их поэлементных произведений:

          _n
   a^Tb  = ∑ a_i * b_i      (3.14)
         ⁱ⁼¹

Векторы размерности n (то есть определённые в пространстве R_n) имеют также геометрическую интерпретацию. Можно показать, что

    a^Tb = | a | * | b | * cos(α),	(3.15)

где α - угол между векторами а и b, а символы | | обозначают модуль (евклидову норму, абсолютную величину, длину) вектора:

             _{__________________}
    | а | = √(a₁² +... + a_n²). (3.16)

Если A и B - матрицы размерностей n*m и m*p соответственно, то их произведение C = A * B - матрица размерности n*p, элементы которой определяются как

                                                       _m
   c_i,j = a_i,1 * b_1,j + a_i,2 * b_1,2 + ... + a_i,m * b_m,j = ∑ a_i,k * b_k,j
                                                      ^k=1

При этом число столбцов A (m) должно совпадать с числом строк B. Элемент с, равен скалярному произведению i-й строки A и j-го столбца B (которые можно считать векторами). Например, результатом произведения

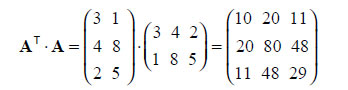
является симметричная матрица, так как она не меняется при транспонировании.

Векторы можно также считать точками. Геометрически сложение двух векторов u и v можно понимать как новый вектор, конечная точка которого - результат "соединения" u и v, как показано на рисунке 1(a).

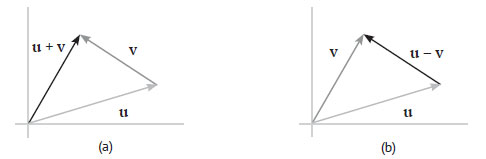
Рис.1. Геометрическая интерпретация сложения и вычитания векторов

Отсюда следует, что вектор, который начинается в конечной точке u и заканчивается в конечной точке v, есть вектор v - u, как показано на рисунке 1(b).

Наконец, двумерный вектор можно повернуть против часовой стрелки на а градусов (или радиан) путём умножения его на матрицу "поворота":


      ⌈  cos(α)   -sin(α) ⌉
  R =                         (3.17)
      ⌊  sin(α)    cos(α) ⌋

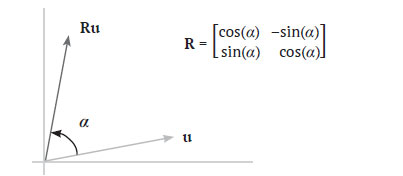
как показано на рисунке 2, где u - вектор-столбец (как обычно принимается в математической литературе).

Рис.2. Матрица поворота (против часовой стрелки)

На следующем шаге мы перейдем к временной сложности вычислений.

Предыдущий шаг Содержание Следующий шаг