На этом шаге мы приведем основные тригонометрические формулы.

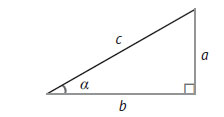
Рис.1. Прямоугольный треугольник как иллюстрация тригонометрических определений

На рис. 1 изображён прямоугольный треугольник, а ниже - связанные с ним основные тригонометрические определения и свойства:

sin(α) = a/c
cos(α) = b/c
tg(α) = sin(α)/cos(α) = a/b
ctg(α) = cos(α)/sin(α) = b/a
sin(0) = 0
cos(0) = 1
sin(30°) = sin(π/6) = 1/2
cos(30°) = cos(π/6) = √3/2
sin(45°) = sin(π/4) = √2/2
cos(45°) = cos(π/4) = √2/2
sin(60°) = sin(π/3) = √3/2
cos(60°) = cos(π/3) = 1/2
sin(90°) = sin(π/2) = 1
cos(90°) = cos(π/2) = 0
sin(α) = –sin(–α)
cos(α) = cos(–α)

где sin, cos, tg и ctg обозначают тригонометрические функции синус, косинус, тангенс и котангенс соответственно. В большинстве языков программирования параметр тригонометрических функций измеряется в радианах (1 радиан = 180°/π).

На следующем шаге мы вспомним векторы и матрицы.

Предыдущий шаг Содержание Следующий шаг