На этом шаге мы напомним эти порядки.
Функция T(n) оценки времени выполнения алгоритма может содержать несколько слагаемых, которые по-разному влияют на её значение для заданного размера задачи n. Пусть, например, T(n) = 0,5n2 + 2000n + 50 000. При небольших значениях n все слагаемые почти в равной степени влияют на рост T(n). Однако с увеличением n первое слагаемое (0,5n2) начинает влиять на рост функции значительно больше, чем два других (даже вместе взятых). Следовательно, порядок роста функции характеризуется её старшим членом. На рисунке 1 приведены отдельные графики для 0,5n2 и 2000n + 50 000.
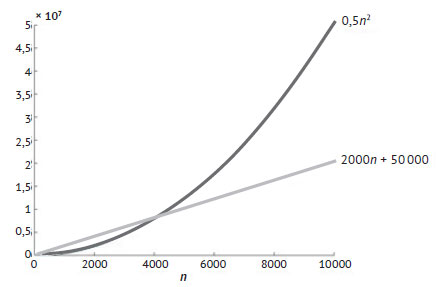
Рис.1. Порядок роста функции определяется её старшим членом. Для T(n) = 0,5n2 + 2000n + 50 000 порядок роста - квадратичный, поскольку для
больших значений n её старший член 0,5n2, очевидно, доминирует над младшими (даже взятыми вместе)
Для больших значений n очевидно, что первое слагаемое доминирует над двумя другими и, следовательно, характеризует скорость роста T(n). Коэффициенты полинома были выбраны так, чтобы показать, что сами они не оказывают существенного влияния на скорость роста функции.
На рисунке 2 приведены графики наиболее распространённых функций, характеризующих порядок роста вычислительной сложности.
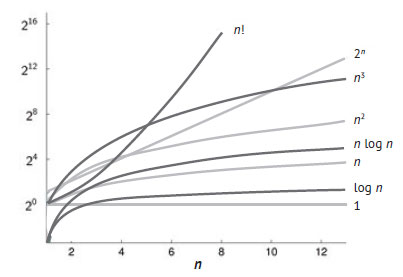
Рис.2. Типичные порядки роста вычислительной сложности
Для достаточно больших значений n их можно упорядочить следующим образом:
1 < log n < n < n log n < n2 < n3 < 2n < n!,
f(n) < g(n), если lim f(n)/g(n) = 0 .
n→∞
Приведённые выше типичные порядки роста называются (слева направо) константными, логарифмическими, линейными, линейно-логарифмическими, квадратичными, кубическими, показательными и факториальными.
Поскольку масштаб оси Y на рисунке 2 - логарифмический, разница между порядками роста может показаться несколько меньше, чем есть на самом деле (каждое следующее деление означает 16-кратный рост времени выполнения алгоритма). В таблице 1 приведены фактические значения этих функций, где явно выделяется быстрый рост показательной и факториальной функций.
| 1 | log2n | n | n*log2n | n2 | n3 | 2n | n! |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 1 | 2 | 1 |
| 1 | 1 | 2 | 2 | 4 | 8 | 4 | 2 |
| 1 | 2 | 4 | 8 | 16 | 64 | 16 | 24 |
| 1 | 3 | 8 | 24 | 64 | 512 | 256 | 40 320 |
| 1 | 4 | 16 | 64 | 256 | 4096 | 65 536 | 2.09*1013 |
| 1 | 5 | 32 | 160 | 1024 | 32 768 | 4 295 967 296 | 2.63*1035 |
Задачи, которые не могут быть решены за полиномиальное время, обычно считаются трудноразрешимыми (трудными), так как время их выполнения довольно велико даже при умеренных размерах. Напротив, задачи, которые могут быть решены за полиномиальное время, считаются легкоразрешимыми (лёгкими). Однако граница между лёгкими и трудными задачами довольно условна. Если время выполнения алгоритма оценивается полиномиальной функцией высокой степени, то на практике может потребоваться довольно много времени для достижения её полного решения или получения промежуточных результатов.
На следующем шаге мы рассмотрим асимптотические обозначения.
