На этом шаге мы обоснуем их использование.
Важной особенностью порядка роста является то, что при его определении обычно пренебрегают постоянными множителями. Подобно слагаемым низших порядков, они опускаются, поскольку с ростом размера задачи их влияние на вычислительную эффективность становится гораздо меньше фактического порядка роста. Более того, нет смысла и в точном определении эффективности алгоритма, поскольку оно зависит от множества факторов, включая аппаратные возможности компьютера, язык программирования, компилятор, интерпретатор и т. д.
Таким образом, на практике достаточно предположить, что для выполнения элементарных машинных команд требуется постоянное время, не имеющее существенного значения.
Теоретический анализ сложности алгоритмов и задач основан на так называемых "асимптотических обозначениях", которые при больших размерах задач позволяют отбрасывать слагаемые низших порядков и постоянные множители. В частности, асимптотические обозначения позволяют определить множества, которые можно использовать для определения "асимптотических границ". Обозначение "Ο" определяется следующим множеством:
Ο(g(n)) = { f(n): ∃с > 0 и n0 > 0 | 0 ≤ f(n) ≤ c ⋅ g(n), ∀n ≥ n0 } .
Если функция f(n) принадлежит этому множеству, то g(n) - асимптотическая верхняя граница f(n). Это означает, что g(n) будет больше f(n), но согласно определению это справедливо только на интервале от некоторого n0 > 0 до бесконечности, причём g(n) может быть умножена на достаточно большую положительную константу с. На рисунке 1(a) приведена графическая иллюстрация этого определения.
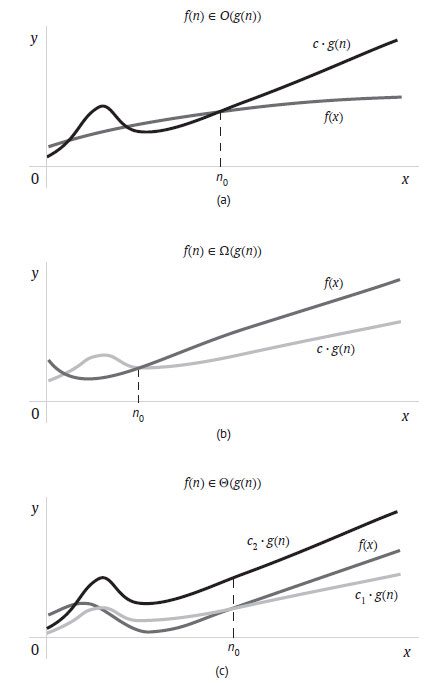
Рис.1. Графическая иллюстрация асимптотических обозначений вычислительной сложности
Если g(n) - асимптотическая верхняя граница f(n), то должна существовать возможность найти такую положительную константу с, что с ⋅ g(n) ≥ f(n), но только для n, не меньшего некоторого положительного значения n0 (то, что происходит при n < n0, не имеет значения). Чтобы доказать, что функция принадлежит Ο(g(n)), достаточно найти хотя бы одну пару (поскольку она не одна) констант с и n0, отвечающих данному определению. Например, если определение верно для некоторой пары с и n0, то оно также верно для бОльших значений с и n0. В связи с этим нет необходимости искать самые маленькие значения с и n0, отвечающие определению O (то же справедливо для всех обозначений, приводимых ниже).
Эффективность алгоритмов чаще всего определяется так называемым худшим случаем, когда среди задач одинакового размера выбирается та, что может потребовать наибольшего количества ресурсов (времени, памяти и т. д.). Поскольку обозначение "Ο" определяет асимптотическую верхнюю границу, оно гарантирует, что конкретному алгоритму даже при больших размерах задачи потребуется в самом худшем случае не более определенного количества ресурсов. Например, время выполнения алгоритма quicksort, сортирующего список или массив из n элементов, вообще говоря, оценивается как Ο(n2), поскольку в худшем случае он требует порядка n2 сравнений. Однако в лучших и умеренных случаях quicksort может работать быстрее (за время порядка n log n).
Напротив, обозначение "Ω" определяет асимптотическую нижнюю границу:
Ω(g(n)) = { f(n): ∃с > 0 и n0 > 0 | 0 ≤ с ⋅ g(n) ≤ f(n), ∀n ≥ n0 } .
На рисунке 1(a) приведена графическая иллюстрация этого определения. Обозначение "Ω" полезно для определения нижней границы ресурсов, необходимых для решения задачи, независимо от применяемого алгоритма. Например, можно теоретически доказать, что любой алгоритм сортировки списка из n вещественных чисел требует в худшем случае Ω(n log n) сравнений.
Наконец, обозначение "Θ" определяет асимптотические жёсткие границы:
Θ(g(n)) = { f(n): ∃с1 > 0, с2 > 0 и n0 > 0 | 0 ≤ с1 ⋅ g(n) ≤ f(n) ≤ с2 ⋅ g(n), ∀n ≥ n0 }.
Если f(n) ∈ Θ(g(n)), то f(n) и g(n) имеют примерно одинаковый порядок роста. Таким образом, g(n) при определённых значениях констант с1 и с2 будет для f(n) и верхней, и нижней асимптотической границей, как показано на рисунке 1(c). Иными словами, f(n) ∈ Ο(g(n)) и f(n) ∈ Ω(g(n)).
Например, алгоритм сортировки слиянием для списка или массива из n элементов всегда требует (в лучшем и худшем случаях) порядка n*log n сравнений. Поэтому мы говорим, что его время выполнения - Θ(n log n).
При определении асимптотических границ константами и слагаемыми низших порядков в функции g(n) пренебрегают. Например, несмотря на очевидность того, что 3n2 + 10n ∈ Ο(5n2 + 20n), достаточно сказать, что 3n2 + 10n ∈ Ο(n2), поскольку для асимптотических обозначений важен лишь порядок роста. В связи с этим вы, видимо, обратили внимание на отсутствие основания логарифма в обозначении порядка роста функции. Причина тому - то, что логарифмы с разными основаниями отличаются только постоянным множителем. Пусть р представляет собой некоторую асимптотическую границу, а a и b - два разных основания логарифмов. Следующие равенства показывают, что все логарифмы независимо от их основания имеют один и тот же порядок:
константа
р loga g(n) = р logb g(n)/logb a = р ⋅ 1logb a logb g(n) = р logb g(n).
Таким образом, в обозначении порядка роста основание логарифма не нужно.
Наконец, при определении порядка роста функции можно использовать пределы благодаря следующим равносильным утверждениям, связывающим их с определениями асимптотических обозначений границ:
f(n) ∈ Ο(g(n)) ⇔ lim f(n)/g(n) < ∞ (константа или ноль),
n→∞
f(n) ∈ Ω(g(n)) ⇔ lim f(n)/g(n) > 0 (константа > 0 или ∞),
n→∞
f(n) ∈ Θ(g(n)) ⇔ lim f(n)/g(n) = константа > 0.
n→∞
На следующем шаге мы поговорим о рекррентных соотношениях.
