На этом шаге мы рассмотрим рекурсивные способы вычисления такой функции.

Следующий пример относится к вычислению двойной суммы вида:

               _{m    n}
    f (m, n) = ∑  ∑ (i + j)    (4.3)
               ^{i=1 j=1}

Пользуясь свойствами сумм, она может быть сведена к простому выражению:

               _{m   n}             _m
    f (m, n) = ∑  ∑ (i + j)  = ∑ (i * n + n(n + 1)/2 = 
               ^{i=1 j=1}           ⁱ⁼¹
             = nm(m + 1)/2 + mn(n + 1)/2 = mn(m + n + 2)/2.

Однако мы решим эту задачу рекурсивно с использованием двух рекурсивных функций (по одной на каждую сумму).

Во-первых, внешняя сумма - функция параметров m и n, размер которой - m. Функция возвращает 0 для её начального условия, когда m меньше наименьшего индекса (то есть когда m ≤ 0). Общая схема для рекурсивного условия в предположении, что размер подзадачи m - 1:

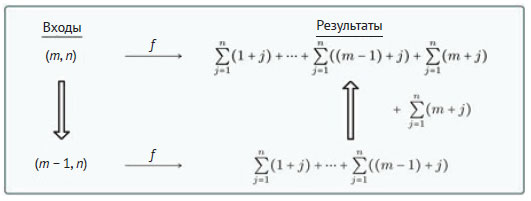
Очевидно, всё, что нужно сделать с результатом f(m - 1, n) для получения f(m, n), - это добавить к нему внутреннюю сумму

               _n
    f (m, n) = ∑ (m + j)   ,
              ^j=1

которую можно считать функцией g(), зависящей от n и m. Поэтому f() можно определить следующим образом:

               0,                     если m ≤ 0,
    f(n, m) = 
               f(m - 1, n) + g(n, m), если m > 0.

Функцию g(n, m) тоже можно определить рекурсивно. Во-первых, поскольку она складывает n слагаемых, её размер равен n. Как и все суммы, она возвращает 0 в начальном условии, которое имеет место при n ≤ 0. Общая схема ее рекурсивного условия, также уменьшающего размер задачи на единицу:

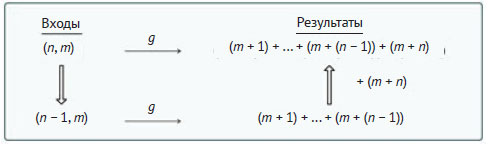
Из схемы видно, что для получения g(n, m) нужно добавить (m + n) к результату подзадачи. Таким образом, функция g() имеет вид:

               0,   если n ≤ 0,
    g(n, m) = 
               g(n - 1, m) + (n + m), если n > 0.

В примере 4.8 приведена реализация обеих сумм.

Пример 4.8. Рекурсивные функции вычисления двойной суммы (4.3)

1
2
3
4
5
6
7
8
9
10
11
12

def inner_sum(n, m):
    if n <= 0:
        return 0
    else:
        return inner_sum(n - 1, m) + (m + n)


def outer_sum(m, n):
    if m <= 0:
        return 0
    else:
        return outer_sum(m - 1, n) + inner_sum(n, m)

Архив с файлом можно взять здесь.

Со следующего шаге мы начнем рассматривать системы счисления.

Предыдущий шаг Содержание Следующий шаг